题目内容
已知函数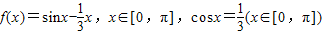 ,那么下面结论正确的是( )
,那么下面结论正确的是( )A.f(x)在[0,x]上是减函数
B.f(x)在[x,π]上是减函数
C.?x∈[0,π],f(x)>f(x)
D.?x∈[0,π],f(x)≥f(x)
【答案】分析:由函数的解析式f(x)=sinx- x可求其导数f′(x)=cosx-
x可求其导数f′(x)=cosx- ,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性.
,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性.
解答:解:∵f(x)=sinx- x
x
∴f′(x)=cosx-
∵cosx= ,x∈[0,π]
,x∈[0,π]
又∵余弦函数y=cosx在区间[0,π]上单调递减
∴当x>x时,cosx<cosx0 即cosx<
∴当x>x时,f′(x)=cosx- <0
<0
∴f(x)=sinx- x在[x,π]上是减函数.
x在[x,π]上是减函数.
故选B.
点评:利用导数判断函数的单调性,一定要注意其方法及步骤.(1)确定函数f(x)的定义域;(2)求导数f′(x);(3)在f(x)的定义域内解不等式f′(x)>0和f′(x)<0;(4)写出f(x)的单调区间.
 x可求其导数f′(x)=cosx-
x可求其导数f′(x)=cosx- ,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性.
,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性.解答:解:∵f(x)=sinx-
 x
x∴f′(x)=cosx-

∵cosx=
 ,x∈[0,π]
,x∈[0,π]又∵余弦函数y=cosx在区间[0,π]上单调递减
∴当x>x时,cosx<cosx0 即cosx<

∴当x>x时,f′(x)=cosx-
 <0
<0 ∴f(x)=sinx-
 x在[x,π]上是减函数.
x在[x,π]上是减函数.故选B.
点评:利用导数判断函数的单调性,一定要注意其方法及步骤.(1)确定函数f(x)的定义域;(2)求导数f′(x);(3)在f(x)的定义域内解不等式f′(x)>0和f′(x)<0;(4)写出f(x)的单调区间.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
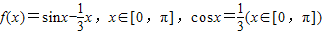 ,那么下面结论正确的是( )
,那么下面结论正确的是( )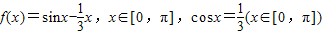 ,那么下面结论正确的是( )
,那么下面结论正确的是( ) ,那么下面结论正确的是( )
,那么下面结论正确的是( )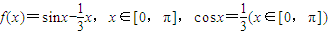 ,那么下面结论正确的是( )
,那么下面结论正确的是( )