题目内容
已知函数f（x）=sin（2x-
）-m在
上两个零点，则m的取值范围为
- A.
- B.
- C.
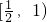
- D.
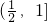
C
分析：利用正弦函数的性质即可求得x∈[0，
]时g（x）=sin（2x-）的取值范围，从而可得函数f（x）=sin（2x-）-m在[0，]上两个零点时m的取值范围．
解答：
解：∵x∈[0，]，
∴2x-∈[-，
]，
∴sin（2x-）∈[-
，1]，
令z=2x-，y=m，
在同一直角坐标系中作出y=sinz（z∈[-，]）与y=m的图象，
由图象可知，≤m＜1时，y=sinz（z∈[-，]）与y=m有两个交点，即函数f（x）=sin（2x-）-m在上有两个零点．
故选C．
点评：本题考查正弦函数的单调性质，求得x∈[0，]时g（x）=sin（2x-）的取值范围是关键，属于中档题．
分析：利用正弦函数的性质即可求得x∈[0，
]时g（x）=sin（2x-）的取值范围，从而可得函数f（x）=sin（2x-）-m在[0，]上两个零点时m的取值范围．解答：
解：∵x∈[0，]，∴2x-
∈[-，]，∴sin（2x-
）∈[-，1]，令z=2x-
，y=m，在同一直角坐标系中作出y=sinz（z∈[-
，]）与y=m的图象，由图象可知，
≤m＜1时，y=sinz（z∈[-，]）与y=m有两个交点，即函数f（x）=sin（2x-）-m在上有两个零点．故选C．
点评：本题考查正弦函数的单调性质，求得x∈[0，
]时g（x）=sin（2x-）的取值范围是关键，属于中档题． 
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
