题目内容
17．奇函数f（x）是定义域为R的周期函数，其周期为4，当x∈（-2，0）时f（x）=2x，f（2012）-f（2011）=-$\frac{1}{2}$．分析 根据函数的周期性可得f（2012）-f（2011）=f（0）-f（-1），结合函数的奇偶性及x∈（-2，0）时f（x）=2x，进而得到答案．
解答 解：∵奇函数f（x）是定义域为R的周期函数，其周期为4，
且当x∈（-2，0）时，f（x）=2x，
∴f（0）=0，f（-1）=$\frac{1}{2}$，
∴f（2012）-f（2011）=f（0）-f（-1）=0-$\frac{1}{2}$=-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．
点评 本题考查的知识点是函数的周期性，函数求值，难度不大，属于基础题．
练习册系列答案
相关题目
几何体的三视图如图所示，则该几何体的体积为28．
12．已知直线l1：y=2x+1，${l_2}：y=-\frac{1}{2}x-2$则两条直线的位置关系为（ ）
| A． | 平行 | B． | 重合 | C． | 相交但不垂直 | D． | 垂直 |
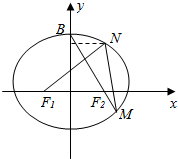如图，已知F1、F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，顶点B的坐标是（0，b），连接BF2并延长交椭圆于点M，点M关于x轴的对称点为N，连接F1、N．