题目内容
（2012•黄冈模拟）如图所示，图中曲线方程为y=x2-1，借助定积分表达围成的封闭图形的面积（ ）分析：由y=x2-1，直线x=0，x=2和x轴围成的封闭图形，然后利用定积分表示区域面积，然后利用定积分的几何意义进行求解即可．
解答：
解：由曲线y=x2-1，直线x=0，x=2和x轴围成的封闭图形的面积为
S=∫01（1-x2）dx+∫12（x2-1）dx
根据对称性，它和函数y=|x2-1|，直线x=0，x=2和x轴围成的封闭图形的面积相等，如图所示．
即S=
|x2-1|dx
故选C．
解：由曲线y=x2-1，直线x=0，x=2和x轴围成的封闭图形的面积为S=∫01（1-x2）dx+∫12（x2-1）dx
根据对称性，它和函数y=|x2-1|，直线x=0，x=2和x轴围成的封闭图形的面积相等，如图所示．
即S=
| ∫ | 2 0 |
故选C．
点评：本题主要考查了利用定积分求面积，同时考查了定积分的几何意义，属于中档题．
练习册系列答案
相关题目
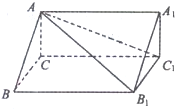（2012•黄冈模拟）如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，AA1=