题目内容
在数列{an}中,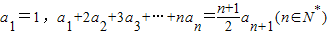 .
.(1)求数列{an}的通项an;
(2)若存在n∈N*,使得an≤(n+1)λ成立,求实数λ的最小值.
【答案】分析:(1)把已知等式中的n换成n-1,再得到一个式子,两式想减可得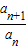 =
=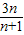 ,求得 a2=1,累乘化简可得数列{an}的通项an .
,求得 a2=1,累乘化简可得数列{an}的通项an .
(2)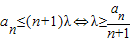 ,由(1)可知当n≥2时,
,由(1)可知当n≥2时,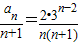 ,
,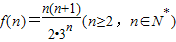 ,可证{
,可证{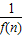 }是递增数列,又
}是递增数列,又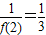 及
及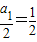 ,
,
可得λ≥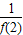 ,由此求得实数λ的最小值.
,由此求得实数λ的最小值.
解答:解:(1)当n≥2时,由a1=1 及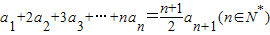 ①可得
①可得
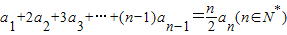 ②.
②.
两式想减可得 nan =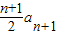 -
-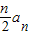 ,化简可得
,化简可得 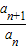 =
=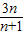 ,∴a2=1.
,∴a2=1.
∴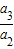 •
•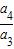 •
•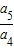 …
…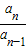 =
=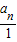 =
= ×
× ×
×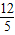 ×…×
×…×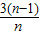 =
=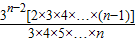 =
=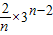 .
.
综上可得,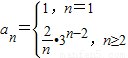 .…(6分)
.…(6分)
(2)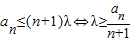 ,由(1)可知当n≥2时,
,由(1)可知当n≥2时,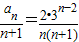 ,
,
设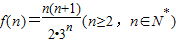 ,…(8分)
,…(8分)
则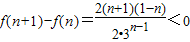 ,
,
∴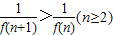 ,
,
故当n≥2时,{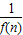 }是递增数列.
}是递增数列.
又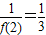 及
及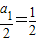 ,可得λ≥
,可得λ≥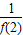 ,所以所求实数λ的最小值为
,所以所求实数λ的最小值为 .…(12分)
.…(12分)
点评:本题主要考查利用数列的递推关系求数列的通项公式,数列与不等式综合,数列的函数特性的应用,属于难题.
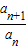 =
=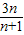 ,求得 a2=1,累乘化简可得数列{an}的通项an .
,求得 a2=1,累乘化简可得数列{an}的通项an .(2)
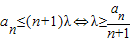 ,由(1)可知当n≥2时,
,由(1)可知当n≥2时,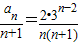 ,
,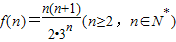 ,可证{
,可证{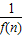 }是递增数列,又
}是递增数列,又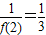 及
及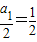 ,
,可得λ≥
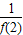 ,由此求得实数λ的最小值.
,由此求得实数λ的最小值.解答:解:(1)当n≥2时,由a1=1 及
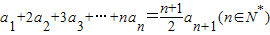 ①可得
①可得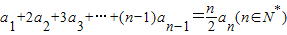 ②.
②.两式想减可得 nan =
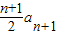 -
-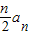 ,化简可得
,化简可得 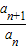 =
=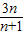 ,∴a2=1.
,∴a2=1.∴
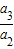 •
•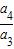 •
•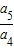 …
…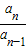 =
=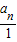 =
= ×
× ×
×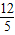 ×…×
×…×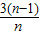 =
=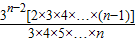 =
=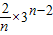 .
.综上可得,
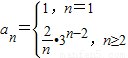 .…(6分)
.…(6分)(2)
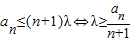 ,由(1)可知当n≥2时,
,由(1)可知当n≥2时,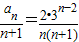 ,
,设
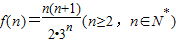 ,…(8分)
,…(8分)则
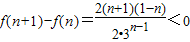 ,
,∴
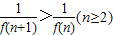 ,
,故当n≥2时,{
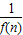 }是递增数列.
}是递增数列.又
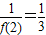 及
及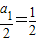 ,可得λ≥
,可得λ≥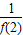 ,所以所求实数λ的最小值为
,所以所求实数λ的最小值为 .…(12分)
.…(12分)点评:本题主要考查利用数列的递推关系求数列的通项公式,数列与不等式综合,数列的函数特性的应用,属于难题.

练习册系列答案
相关题目