题目内容
定义在![]() 上的函数
上的函数![]() 满足
满足![]() 且当
且当![]() 时,
时,
都有![]() ;
;
(1)判断![]() 在
在![]() 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(2)若![]() 是奇函数, 不等式
是奇函数, 不等式![]() 对所有的
对所有的![]() 恒成立,
恒成立,
求![]() 的取值范围.
的取值范围.
(1)见解析 (2)![]() 或
或![]() .
.
解析:
(1)证明:设![]() 令
令![]() ,
,
则![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() 在[-1,1]上是增函数.
在[-1,1]上是增函数.
(2)当![]() 时,
时, ![]() 不成立(舍去)
不成立(舍去)
当![]() 时,
时, ![]() 在[-1,1]上是增函数,
在[-1,1]上是增函数, ![]()
![]()
![]()
![]()
当![]() 时,
时, ![]() 是奇函数,
是奇函数, ![]() ,
,![]() ,
,
![]()
![]()
![]()
综上所述: ![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的函数
上的函数 满足
满足 且当
且当 时
时
 则
则 的值是
( )
的值是
( )
 上的函数
上的函数 满足
满足 且
且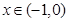 时,
时, 则
则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)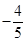
 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则
 B
B
 C
C
 D
D

 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 满足
满足 且
且 时,
时, ,则
,则 ( )
( ) C.
C.
 D.
D.