题目内容
(2013•天河区三模)以下三个命题:
①若|a-b|<1,则|a|<|b|+1;
②若a,b∈R,则|a+b|-2|a|≤|a-b|;
③若|x|<2,|y|>3,则|
|<
,
其中正确命题的序号是
①若|a-b|<1,则|a|<|b|+1;
②若a,b∈R,则|a+b|-2|a|≤|a-b|;
③若|x|<2,|y|>3,则|
| x |
| y |
| 2 |
| 3 |
其中正确命题的序号是
①②③
①②③
.分析:利用绝对值三角不等式判断①的正误;绝对值不等式判断②的正误;不等式的性质判断③的正误;
解答:解:因为|a-b|<1,所以|a|-|b|<1,则|a|<|b|+1,所以①正确;
若a,b∈R,则|a+b|-2|a|≤|a-b|;所以|a+b|-2|a|≤a+b-2a|=|a-b|;所以②正确;
若|x|<2,|y|>3,0<
<
,所以|
|<
,③正确;
正确命题的序号:①②③.
故答案为:①②③.
若a,b∈R,则|a+b|-2|a|≤|a-b|;所以|a+b|-2|a|≤a+b-2a|=|a-b|;所以②正确;
若|x|<2,|y|>3,0<
| 1 |
| |y| |
| 1 |
| 3 |
| x |
| y |
| 2 |
| 3 |
正确命题的序号:①②③.
故答案为:①②③.
点评:本题考查绝对值三角不等式的应用,不等式的基本性质的考查.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
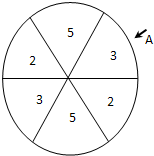 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).