题目内容
已知函数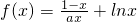 .
.
(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求正实数a的取值范围;
(Ⅱ)若a=1,k∈R且 ,设F(x)=f(x)+(k-1)lnx,求函数F(x)在
,设F(x)=f(x)+(k-1)lnx,求函数F(x)在 上的最大值和最小值.
上的最大值和最小值.
解:(Ⅰ)由题设可得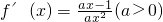
因为函数f(x)在[1,+∞)上是增函数,所以当x∈[1,+∞)时,不等式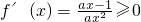 ,即
,即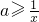 恒成立
恒成立
因为当x∈[1,+∞)时, 的最大值为1,所以实数a的取值范围是[1,+∞)
的最大值为1,所以实数a的取值范围是[1,+∞)
(Ⅱ)a=1时,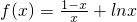 ,
,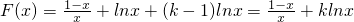
所以,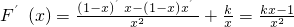 …
…
(1)若k=0,则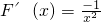 ,在
,在 上,恒有F'(x)<0,所以F(x)在
上,恒有F'(x)<0,所以F(x)在 上单调递减
上单调递减
∴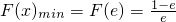 ,
,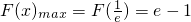
(2)k≠0时,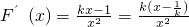
(i)若k<0,在 上,恒有
上,恒有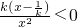 ,所以F(x)在
,所以F(x)在 上单调递减
上单调递减
∴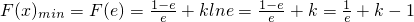 ,
,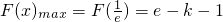
(ii)k>0时,因为 ,所以
,所以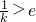
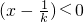 ,所以
,所以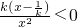 ,所以F(x)在
,所以F(x)在 上单调递减
上单调递减
∴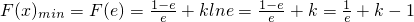 ,
,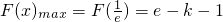
综上所述:当k=0时,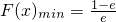 ,F(x)max=e-1;当k≠0且
,F(x)max=e-1;当k≠0且 时,F(x)max=e-k-1,
时,F(x)max=e-k-1,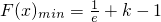
分析:(Ⅰ)求导函数
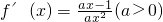 ,利用函数f(x)在[1,+∞)上是增函数,可得x∈[1,+∞)时,不等式
,利用函数f(x)在[1,+∞)上是增函数,可得x∈[1,+∞)时,不等式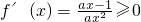 ,即
,即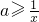 恒成立,求出右边函数的最大值,即可求得实数a的取值范围;
恒成立,求出右边函数的最大值,即可求得实数a的取值范围;(Ⅱ)a=1时,
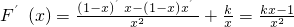 ,分类讨论:(1)若k=0,F(x)在
,分类讨论:(1)若k=0,F(x)在 上单调递减;(2)k≠0时,
上单调递减;(2)k≠0时,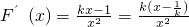 ,确定函数的单调性,即可求得函数的最值.
,确定函数的单调性,即可求得函数的最值.点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查函数的最值,考查分类讨论的数学思想,正确求导,恰当分类是关键.

 名校课堂系列答案
名校课堂系列答案已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数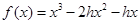 ,若
,若 且
且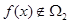 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得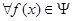 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


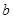
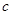




 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.