题目内容
设集合A={x||x-a|＜2}，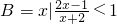
，且A⊆B，则实数a的取值范围是________．
[0，1]
分析：解绝对值不等式化简集合A，解分式不等式化简集合B，根据A⊆B，考查集合端点间的大小关系，求出实数a的取值范围．
解答：集合A={x||x-a|＜2}={x|-2＜x-a＜2}={x|a-2＜x＜a+2}，
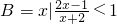={x|
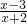＜0}={x|（x-3）（x+2）＜0}={x|-2＜x＜3}．
∵A⊆B，
∴
，解得 0≤a≤1．
故答案为[0，1]．
点评：本题主要考查绝对值不等式的解法，分式不等式的解法，集合中参数的取值问题，体现了化归与转化的数学思想，
属于中档题．
分析：解绝对值不等式化简集合A，解分式不等式化简集合B，根据A⊆B，考查集合端点间的大小关系，求出实数a的取值范围．
解答：集合A={x||x-a|＜2}={x|-2＜x-a＜2}={x|a-2＜x＜a+2}，
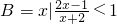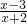={x|＜0}={x|（x-3）（x+2）＜0}={x|-2＜x＜3}．∵A⊆B，
∴
，解得 0≤a≤1．故答案为[0，1]．
点评：本题主要考查绝对值不等式的解法，分式不等式的解法，集合中参数的取值问题，体现了化归与转化的数学思想，
属于中档题．
练习册系列答案
相关题目
设集合A={x|x+1＞0}，集合B={x|x2-2＜0}则A∪B等于（ ）
A、{x|x＜-1或x＞
| ||
B、{x|-1＜x＜
| ||
C、{x|x＞-
| ||
| D、{x|x＞-1} |
设集合A={x|x2-3x+2=0}，B={y|y=x2-2x+3，x∈A}，现在我们定义对于任意两个集合M，N的运算：M?N={x|x∈M∪N，且x?M∩N}，则A?B=（ ）
| A、{1，2，3} | B、{1，2} | C、{2，3} | D、{1，3} |