题目内容
已知函数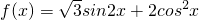 .
.
(I) 求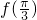 ;
;
(II)求函数f(x)的最小正周期和单调递增区间.
解:(I)依题意f(x)=
=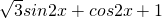 .
.
=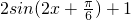 .
.
∴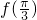 =
= .
.
(II)设函数f(x)的最小正周期为T,则 T=π.
由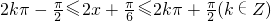 ,解得
,解得 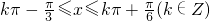 ,
,
∴函数的单调递增区间为[ ,k∈z.
,k∈z.
分析:(I)利用两角和差的正弦公式的应用,二倍角公式,化简函数f(x)的解析式为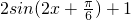 ,由此求得
,由此求得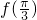 的值.
的值.
(II)根据函数f(x)的解析式求出周期,由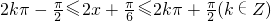 ,解得x的范围,即得函数的单调递增区间.
,解得x的范围,即得函数的单调递增区间.
点评:本题主要考查两角和差的正弦公式的应用,二倍角公式,正弦函数的单调性和周期性,化简函数f(x)的解析式为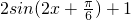 ,是解题的关键.
,是解题的关键.

=
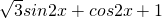 .
.=
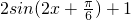 .
.∴
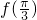 =
= .
.(II)设函数f(x)的最小正周期为T,则 T=π.
由
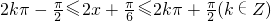 ,解得
,解得 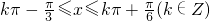 ,
,∴函数的单调递增区间为[
 ,k∈z.
,k∈z.分析:(I)利用两角和差的正弦公式的应用,二倍角公式,化简函数f(x)的解析式为
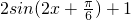 ,由此求得
,由此求得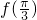 的值.
的值.(II)根据函数f(x)的解析式求出周期,由
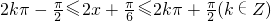 ,解得x的范围,即得函数的单调递增区间.
,解得x的范围,即得函数的单调递增区间.点评:本题主要考查两角和差的正弦公式的应用,二倍角公式,正弦函数的单调性和周期性,化简函数f(x)的解析式为
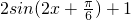 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 .
. ,,求△ABC的面积.
,,求△ABC的面积. .
. .
. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
. 的值;
的值;