题目内容
若在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 有派驻点
有派驻点![]() .
.
(1)问函数![]() 是否有派驻点?请说明理由;
是否有派驻点?请说明理由;
(2)证明函数![]() 有派驻点;
有派驻点;
(3)若函数![]() 有派驻点,求实数
有派驻点,求实数![]() 的取值范围.
的取值范围.
解:⑴假设函数![]() 有派驻点
有派驻点![]() ,则
,则![]() ,即
,即![]() ,而此方程无实根,矛盾.所以函数
,而此方程无实根,矛盾.所以函数![]() 没有派驻点. ………………… 4分
没有派驻点. ………………… 4分
⑵令![]() ,又
,又![]() ,
,![]() ,
, ![]()
![]() ,所以
,所以![]() 在
在![]() 上至少有一个实根
上至少有一个实根![]() ,即函数
,即函数![]() 有派驻点
有派驻点![]() . ……………………………… 9分
. ……………………………… 9分
⑶若函数![]() 有派驻点
有派驻点![]() ,即有:
,即有:![]() 成立.
成立.![]() 又
又![]()
![]()
设![]() ,则由
,则由![]() 得
得![]() ,列表:
,列表:
|
|
|
|
|
|
|
|
| + | 0 | — | 0 | + |
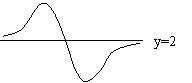 又极大值为
又极大值为![]() ;极小值为
;极小值为![]() ;
;
![]() ,所以
,所以![]() 的值域为
的值域为![]() ,
,
即![]() 的范围是
的范围是![]() . …………………………… 14分
. …………………………… 14分

练习册系列答案
相关题目
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断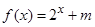 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;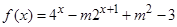 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数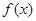 ,若在定义域内存在实数
,若在定义域内存在实数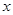 ,满足
,满足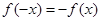 ,则称
,则称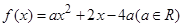 ,试判断
,试判断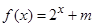 是定义在区间
是定义在区间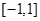 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数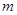 的取值范围;
的取值范围; 为定义域
为定义域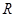 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数