Question

存在两条直线x=±m与双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）相交于四点A，B，C，D，且四边形ABCD为正方形，则双曲线的离心率的取值范围为

（

2

，+∞）

．

Answer 1

分析：根据题意，双曲线与直线y=±x相交且有四个交点，由此得

b

a

＞1，结合双曲线的基本量的平方关系和离心率的定义，化简整理即得该双曲线的离心率的取值范围．

解答：解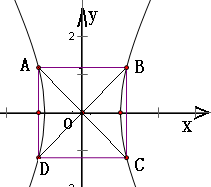：∵四边形ABCD为正方形，
∴对角线AC、BD所在直线是各象限的角平分线
因此，直线y=±x与双曲线

x2

a2

-

y2

b2

=1有四个交点
∴双曲线的渐近线y=±

b

a

x，满足

b

a

＞1，
即b＞a，平方得：b²＞a²，c²-a²＞a²，可得c²＞2a²，
两边都除以a²，得

c2

a2

＞2，即e²＞2，
∴e＞

2

，即双曲线的离心率的取值范围是（

2

，+∞）
故答案为：（

2

，+∞）

点评：本题给出双曲线上四个点构成以原点为中心的正方形，求它的离心率取值范围，着重考查了双曲线的标准方程和简单几何性质等知识，属于基础题．