Question

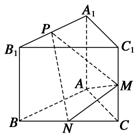
二面角M-l-N的大小为60°, 面M内有点A, A在N内的射影为C, A在l上的射影为E, CE＝a; 面N内有点B, B在M内的射影为D, B在l上的射影为F, DF＝b; EF＝2c, 则AB的长为

[　　]

A.2　　B.2

C.　　  D. 

Answer 1

答案：B
解析：

解:  由条件有AE⊥l , AC⊥平面N,  由三垂线定理的逆定理得 CE⊥l,  所以∠AEC是二面角M--N的平面角, 由此得∠AEC＝60°. 又已知CE＝a, 从Rt△ACE得AE＝2a. 同理可得BF＝2b. 由BF和CE都在平面N内, 并且都垂直于l, 得BF∥CE, 所以异面直线AE和BF的夹角是60°, 并且EF是它们的公垂线, 利用异面直线上两点间距离的公式, 得

提示：

用异面直线上两点间距离公式.