题目内容
已知x2-20x+64≤0的解集为A,当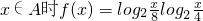 的值域为B.
的值域为B.
(1)求集合B;
(2)当x∈B时不等式1+2x+4xa≥0恒成立,求a的最小值.
解:(1)A={x|4≤x≤16}
f(x)=(log2x-3)(log2x-2)=(log2x)2-5log2x+6
令t=log2x,则t∈[2,4],
∵t∈[2,4],
∴ 时,y取得最小值
时,y取得最小值 ,t=4时,y取得最大值2
,t=4时,y取得最大值2
∴
(2)分离参数可得:
设
当x∈B时不等式1+2x+4xa≥0恒成立,可转化为a≥g(x)max
∵ 在
在 上递增
上递增
∴
∴
分析:(1)先化简集合A,再利用对数的运算法则,化简函数,利用换元法,转化为二次函数的最值,求出集合B;
(2)分离参数,将当x∈B时不等式1+2x+4xa≥0恒成立,转化为a≥g(x)max即可.
点评:本题以集合为载体,考查函数的值域,考查恒成立问题,解题的关键是转化为二次函数的最值,利用分离参数法解决恒成立问题.
f(x)=(log2x-3)(log2x-2)=(log2x)2-5log2x+6
令t=log2x,则t∈[2,4],

∵t∈[2,4],
∴
 时,y取得最小值
时,y取得最小值 ,t=4时,y取得最大值2
,t=4时,y取得最大值2∴

(2)分离参数可得:

设

当x∈B时不等式1+2x+4xa≥0恒成立,可转化为a≥g(x)max
∵
 在
在 上递增
上递增∴

∴

分析:(1)先化简集合A,再利用对数的运算法则,化简函数,利用换元法,转化为二次函数的最值,求出集合B;
(2)分离参数,将当x∈B时不等式1+2x+4xa≥0恒成立,转化为a≥g(x)max即可.
点评:本题以集合为载体,考查函数的值域,考查恒成立问题,解题的关键是转化为二次函数的最值,利用分离参数法解决恒成立问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
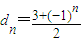 ,数列{an}满足an=d1+d2+d3+…+d2n;数列{bn}为公比大于1的等比数列,且b2,b4为方程x2-20x+64=0的两个不相等的实根.
,数列{an}满足an=d1+d2+d3+…+d2n;数列{bn}为公比大于1的等比数列,且b2,b4为方程x2-20x+64=0的两个不相等的实根.