题目内容
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
A,B两种产品各生产20、24吨时,利润最大为340万元.
解析试题分析:设生产A,B两种产品各为x,y吨,利润为z万元。根据已知条件可以得出关于 间的不等式组即线性约束条件(注意:根据实际意义
间的不等式组即线性约束条件(注意:根据实际意义 均应大于等于0),再用
均应大于等于0),再用 表示出
表示出 即目标函数。画出线性约束条件表示的可行域,再画出目标函数线将其平移使其经过可行域,当目标函数线的纵截距最大时
即目标函数。画出线性约束条件表示的可行域,再画出目标函数线将其平移使其经过可行域,当目标函数线的纵截距最大时 也最大。
也最大。
解 设生产 两种产品各为
两种产品各为 吨,利润为
吨,利润为 万元,则
万元,则 ,
, 

作出可行域(如图),作出在一组平行直线 (
( 为参数),此直线经过
为参数),此直线经过 ,故
,故
的最优解为 ,
, 的最大值为
的最大值为 (万元).
(万元).
考点:线性规划。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,求目标函数z=6x+10y的最大值是
,求目标函数z=6x+10y的最大值是  中,已知点
中,已知点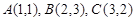 ,点
,点 在
在 三边围成的区域(含边界)上
三边围成的区域(含边界)上 ,求
,求 ;
; ,用
,用 表示
表示 ,并求
,并求 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
. 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值;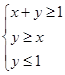 上的一个动点,试确定角
上的一个动点,试确定角 cm2的内接矩形玻璃(阴影部分),则其边长
cm2的内接矩形玻璃(阴影部分),则其边长 (单位:cm)的取值范围是( )
(单位:cm)的取值范围是( )




 满足不等式组
满足不等式组 则
则 的最小值是 ,最大值是
的最小值是 ,最大值是