题目内容
【题目】已知![]() ,
, ![]() 是
是![]() 的导函数.
的导函数.
(1)求![]() 的极值;
的极值;
(2)证明:对任意实数![]() ,都有
,都有![]() 恒成立;
恒成立;
(3)若![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)由题意得处![]() ,进而
,进而![]() ,分
,分![]() 和
和![]() 两种情况讨论,即可求解;
两种情况讨论,即可求解;
(Ⅱ)由![]() ,则要证
,则要证![]()
![]() ,只需证
,只需证![]() .
.
令![]() ,利用导数得出函数
,利用导数得出函数![]() 的性质,即可作出证明.
的性质,即可作出证明.
(Ⅲ)由(Ⅱ)知![]() 恒成立,可得
恒成立,可得![]() ,分
,分![]() 和
和![]() 两种情况讨论,即可求解实数
两种情况讨论,即可求解实数![]() 的值.
的值.
试题解析:
(Ⅰ)![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 无极值;
无极值;
当![]() 时,
时, ![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以当![]() 时,有极小值
时,有极小值![]() .
.
(Ⅱ)因为![]() ,所以,要证
,所以,要证![]()
![]() ,只需证
,只需证![]() .
.
令![]() ,则
,则![]() ,且
,且![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() 恒成立,
恒成立,
∴对任意实数![]() ,都有
,都有![]()
![]() 恒成立.
恒成立.
(Ⅲ)令![]() ,则
,则![]() ,注意到
,注意到![]() ,
,
由(Ⅱ)知![]() 恒成立,故
恒成立,故![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() ,
,
于是当![]() 时,
时, ![]() ,即
,即![]() 成立.
成立.
②当![]() 时,由
时,由![]() (
(![]() )可得
)可得![]() (
(![]() ).
).
![]() ,
,
故当![]() 时,
时, ![]() ,
,
于是当![]() 时,
时, ![]() ,
, ![]() 不成立.
不成立.
综上, ![]() 的取值范围为
的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校计划面向高一年级1240名学生开设校本选修课程,为确保工作的顺利实施,按性别进行分层抽样,现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查,其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
(1)根据以上数据完成下列列联表;
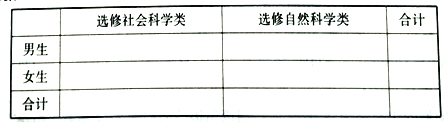
(2)判断能否有99.9%的把握认为科类的选修与性别有关?
附: 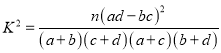 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:现采用分层抽样的方法抽取容量为20的样本.
(1)其中课外体育锻炼时间在![]() 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?
(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在![]() 分钟内的概率.
分钟内的概率.
锻炼时间(分钟) |
|
|
|
|
|
|
人数 | 40 | 60 | 80 | 100 | 80 | 40 |
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1![]() 号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:
号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段: ![]() ;
; ![]() (单位:岁),其猜对歌曲名称与否的人数如图所示.
(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ)写出![]() 列联表;判断是否有
列联表;判断是否有![]() 的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(Ⅱ)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中恰好有一人在![]() 岁之间的概率.
岁之间的概率.
(参考公式:  ,其中
,其中![]() )
)