题目内容
在△ABC中,若a=3,b=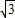 ,
,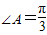 ,则∠C的大小为 .
,则∠C的大小为 .
【答案】分析:利用正弦定理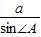 =
=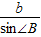 ,可求得∠B,从而可得∠C的大小.
,可求得∠B,从而可得∠C的大小.
解答:解:∵△ABC中,a=3,b=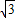 ,
,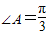 ,
,
∴由正弦定理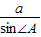 =
=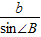 得:
得: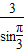 =
=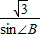 ,
,
∴sin∠B= .又b<a,
.又b<a,
∴∠B<∠A=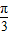 .
.
∴∠B=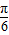 .
.
∴∠C=π-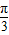 -
-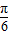 =
=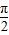 .
.
故答案为: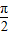 .
.
点评:本题考查正弦定理,求得∠B是关键,易错点在于忽视“△中大变对大角,小边对小角”结论的应用,属于基础题.
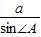 =
=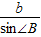 ,可求得∠B,从而可得∠C的大小.
,可求得∠B,从而可得∠C的大小.解答:解:∵△ABC中,a=3,b=
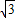 ,
,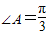 ,
,∴由正弦定理
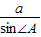 =
=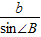 得:
得: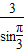 =
=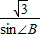 ,
,∴sin∠B=
 .又b<a,
.又b<a,∴∠B<∠A=
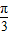 .
.∴∠B=
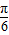 .
.∴∠C=π-
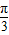 -
-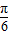 =
=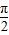 .
.故答案为:
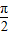 .
.点评:本题考查正弦定理,求得∠B是关键,易错点在于忽视“△中大变对大角,小边对小角”结论的应用,属于基础题.

练习册系列答案
相关题目
在△ABC中,若a=7,b=3,c=8,则其面积等于( )
| A、12 | ||
B、
| ||
| C、28 | ||
D、6
|