题目内容
在极坐标系中,曲线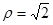 截直线
截直线 所得的弦长为 .
所得的弦长为 .
2
解析试题分析:由曲线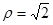 的参数方程化为普通方程为x2+y2=2,其圆心是O(0,0),半径为
的参数方程化为普通方程为x2+y2=2,其圆心是O(0,0),半径为 .
.
由 得:ρcosθ-ρsinθ=
得:ρcosθ-ρsinθ= ,化为直角坐标方程为x-y-
,化为直角坐标方程为x-y- =0,
=0,
由点到直线的距离公式,得弦心距d=1。
故l被曲线C所截得的弦长为2 =2,故答案为2。
=2,故答案为2。
考点:圆的参数方程和直线的极坐标方程与直角坐标方程的互化,直线与圆的位置关系。
点评:中档题,首先完成圆的参数方程和直线的极坐标方程与直角坐标方程的互化,从而“化生为熟”。确定圆的弦长问题。往往利用“特征直角三角形”。

练习册系列答案
相关题目
 为方程
为方程 所表示的曲线上一动点,
所表示的曲线上一动点, ,则
,则 的最小值为 .
的最小值为 . 上的点到直线
上的点到直线 的距离的最大值是 .
的距离的最大值是 . ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为
轴正半轴建立直角坐标系,则该曲线的直角坐标方程为  ,曲线
,曲线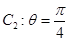 ,若曲线
,若曲线 与
与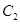 交于
交于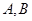 两点,则线段
两点,则线段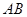 的长度为
的长度为  (t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________.
(t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________. 与直线l关于 直线θ=
与直线l关于 直线θ= (ρ∈R)对称,则l的极坐标方程是 .
(ρ∈R)对称,则l的极坐标方程是 . )=2,则极点在直线l上的射影的极坐标是__________.
)=2,则极点在直线l上的射影的极坐标是__________.