题目内容
若直线y=x+2与曲线y=
(m>0)恰有一个公共点,则实数m的取值范围为 .
| m-x 2 |
分析:曲线y=
(m>0)表示以原点为圆心,
为半径的圆在x轴上方的部分,画出图象,结合图象,即可得出结论.
| m-x 2 |
| m |
解答: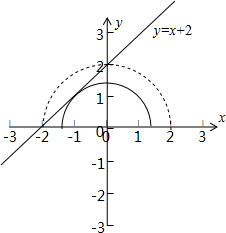 解:曲线y=
解:曲线y=
(m>0)表示以原点为圆心,
为半径的圆在x轴上方的部分,
直线y=x+2与曲线y=
(m>0)相切时,
=
,∴m=2,
直线y=x+2与曲线y=
(m>0)有两个交点时,
将(0,2)代入y=
(m>0),可得m=4,
∴直线y=x+2与曲线y=
(m>0)恰有一个公共点时,实数m的取值范围为m>4或m=2.
故答案为:m>4或m=2.
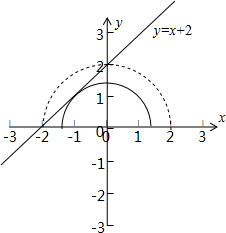 解:曲线y=
解:曲线y=| m-x 2 |
| m |
直线y=x+2与曲线y=
| m-x 2 |
| 2 | ||
|
| m |
直线y=x+2与曲线y=
| m-x 2 |
将(0,2)代入y=
| m-x 2 |
∴直线y=x+2与曲线y=
| m-x 2 |
故答案为:m>4或m=2.
点评:本题考查直线与圆相交的性质,数形结合是解决问题的关键,属中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
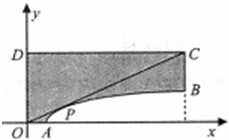 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组