题目内容
如图所示,已知正三棱柱![]() 的各条棱长都为
的各条棱长都为![]() ,P为
,P为![]() 上的点。
上的点。
(1)试确定![]() 的值,使PC
的值,使PC![]() AB;
AB;
(2)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的条件下,求![]() 到平面PAC的距离。
到平面PAC的距离。
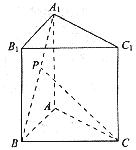
解:(1)当![]() 时,
时,![]() 。取AB的中点O,连接CO、PO。
。取AB的中点O,连接CO、PO。
∵△ABC为正三角形, ∴![]() 。
。
当P为![]() 中点时,PO∥
中点时,PO∥![]() 。∴
。∴![]() ⊥底面ABC ,PO⊥底面ABC,
⊥底面ABC ,PO⊥底面ABC,
PO⊥AB(三垂线定理)。

(2)当![]() 时,过P作PD⊥AB于D,则
时,过P作PD⊥AB于D,则
PD⊥底面ABC,过DE⊥AC于E,连接PE,
则PE⊥AC,∴∠DEP为二面角P―AC―B的平面角,
又∵PD∥![]() ,∴
,∴![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() 。
。
(3)设![]() 到平面PAC的距离为d,则
到平面PAC的距离为d,则![]() ,
,
∵PD∥![]() ,∴PD∥平面
,∴PD∥平面![]() ,DE即为点P到面
,DE即为点P到面![]() 的距离,
的距离,
又![]() 。
。
∴![]() ,
,
从而![]() ,
,
∴![]() ,
,
即![]() 到平面PAC的距离为
到平面PAC的距离为![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
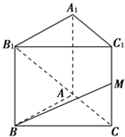 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是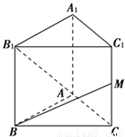 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 . 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .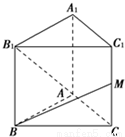 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .