(2013•天河区三模)直线y=2x与抛物线y=x2围成的图形的面积等于4343．题目和参考答案——青夏教育精英家教网—

题目内容

（2013•天河区三模）直线y=2x与抛物线y=x²围成的图形的面积等于

．

分析：本题考查的知识点是定积分的几何意义，首先我们要联立两个曲线的方程，判断他们的交点，以确定积分公式中x的取值范围，再根据定积分的几何意义，所求图形的面积为S=∫₀ ²（ 2x-x²）dx，计算后即得答案．

解答：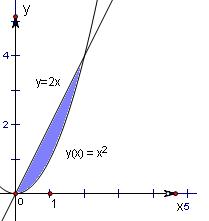

解：由方程组

y=2x

y=x2

，解得，x₁=0，x₂=2．
故所求图形的面积为S=∫₀ ²（ 2x-x²）dx
=（x²-

x³）|₀ ²=

．
故答案为：

点评：在直角坐标系下平面图形的面积的四个步骤：1．作图象；2．求交点；3．用定积分表示所求的面积；4．微积分基本定理求定积分．

练习册系列答案

相关题目

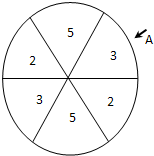（2013•天河区三模）如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A所指区域的数字就是每次游戏所得的分数（箭头指向两个区域的边界时重新转动），且箭头A指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘，得分情况记为（a，b）（假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）．
（Ⅰ）求某个家庭得分为（5，3）的概率？
（Ⅱ）若游戏规定：一个家庭的得分为参与游戏的两人得分之和，且得分大于等于8的家庭可以获得一份奖品．请问某个家庭获奖的概率为多少？
（Ⅲ）若共有5个家庭参加家庭抽奖活动．在（Ⅱ）的条件下，记获奖的家庭数为X，求X的分布列及数学期望．

（2013•天河区三模）已知函数f(x)=

1+lg(x-1)，x＞1

g(x)，x＜1

的图象关于点P对称，且函数y=f（x+1）-1为奇函数，则下列结论：
（1）点P的坐标为（1，1）；
（2）当x∈（-∞，0）时，g（x）＞0恒成立；
（3）关于x的方程f（x）=a，a∈R有且只有两个实根．
其中正确结论的题号为（　　）

（2013•天河区三模）设f（x）是定义在区间（1，+∞）上的函数，其导函数为f'（x）．如果存在实数a和函数h（x），其中h（x）对任意的x∈（1，+∞）都有h（x）＞0，使得f'（x）=h（x）（x²-ax+1），则称函数f（x）具有性质P（a）．
（1）设函数f(x)=Inx+

b+2

x+1

(x＞1)，其中b为实数．
（i）求证：函数f（x）具有性质P（b）；
（ii）求函数f（x）的单调区间．
（2）已知函数g（x）具有性质P（2），给定x₁，x₂∈（1，+∞），x₁＜x₂，设m为实数，a=mx₁+（1-m）x₂，β=（1-m）x₁+mx₂，且a＞1，β＞1，若|g（a）-g（β）|＜|g（x₁）-g（x₂）|，求m取值范围．

（2013•天河区三模）函数y=cosx的图象上各点的横坐标变为原来的

（2013•天河区三模）已知数列{a_n}为等差数列，且a₂+a₇+a₁₂=24，S_n为数列{a_n}的前n项和，n∈N^*，则S₁₃的值为（　　）

试题分类