题目内容
(附加题)
在数列{an}中,a1=1,a n+1=2an+2n.
(1)设bn=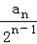 .证明:数列{bn}是等差数列;
.证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn.
解:由a n+1=2an+2n.
两边同除以2n得
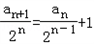
∴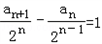 ,
,
即b n+1﹣bn=1
bn以1为首项,1为公差的等差数列
(2)由(1)得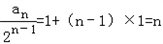
∴an=n 2 n﹣1
2 n﹣1
Sn=20+2×21+3×22+…+n×2 n﹣1
2Sn=21+2×22+…+(n﹣1)2 n﹣1+n×2n
∴﹣Sn=20+21+22+…+2 n﹣1﹣n 2n
2n
=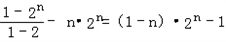
∴Sn=(n﹣1) 2n+1
2n+1
两边同除以2n得
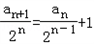
∴
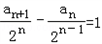 ,
,即b n+1﹣bn=1
bn以1为首项,1为公差的等差数列
(2)由(1)得
∴an=n
 2 n﹣1
2 n﹣1Sn=20+2×21+3×22+…+n×2 n﹣1
2Sn=21+2×22+…+(n﹣1)2 n﹣1+n×2n
∴﹣Sn=20+21+22+…+2 n﹣1﹣n
 2n
2n=
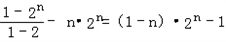
∴Sn=(n﹣1)
 2n+1
2n+1
练习册系列答案
相关题目
 的最小值是_____________
的最小值是_____________ 中,
中, ,
, ,则通项
,则通项 ;
;  的最小值是_____________
的最小值是_____________ |+|PB|最小求出最小值是
|+|PB|最小求出最小值是  中,
中,
 ,
, ,则通项
,则通项 ;
;