题目内容
给出四个命题:
(1)若cosα=cosβ,则α=β;
(2)函数y=2cos(2x+
)的图象关于直线x=-
对称;
(3)函数y=sin|x|是周期函数,且周期为2π;
(4)函数y=cosx(x∈R)为偶函数.
其中所有正确命题的序号是______.
(1)若cosα=cosβ,则α=β;
(2)函数y=2cos(2x+
| π |
| 3 |
| π |
| 6 |
(3)函数y=sin|x|是周期函数,且周期为2π;
(4)函数y=cosx(x∈R)为偶函数.
其中所有正确命题的序号是______.
(1)若cosα=cosβ,则α=β,应该为α=2kπ±β,k∈Z,所以(1)不正确;
(2)x=-
时函数y=2cos(2x+
)=0,所以函数的图象关于直线x=-
对称,不正确;
(3)函数y=sin|x|是周期函数,且周期为2π;应该是:π;不正确;
(4)函数y=cosx(x∈R)为偶函数.是正确的.
故答案为:(4).
(2)x=-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
(3)函数y=sin|x|是周期函数,且周期为2π;应该是:π;不正确;
(4)函数y=cosx(x∈R)为偶函数.是正确的.
故答案为:(4).

练习册系列答案
相关题目
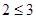 ; (2)如果
; (2)如果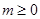 , 则方程
, 则方程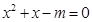 有实根; (3)
有实根; (3)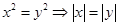 ; (4)“
; (4)“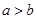 ”是 “
”是 “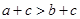 ”的充要条件,其中正确命题的个数有( )个
”的充要条件,其中正确命题的个数有( )个