题目内容
(本小题满分14分)
(1)求证:
(2)求 的展开式的常数项.
的展开式的常数项.
(3)求 的展开式中
的展开式中 的系数
的系数
(1)求证:

(2)求
 的展开式的常数项.
的展开式的常数项. (3)求
 的展开式中
的展开式中 的系数
的系数(1)见解析;(2) ;(3)375.
;(3)375.
 ;(3)375.
;(3)375.第一问中是关于排列数公式的运用。阶乘的求解运算。
第二问中,对于二项式定理的展开式的通项公式先写出,然后令未知数的次数为零即为所求的常数项。
第三问,利用配凑的思想得到,分为三种情况,当第一式取1时,当第一式去x时,当第一式取x2时,分别组合相乘得到。
(1)证明:左边=
= (2分)
(2分)
= =
=
= 右边 (3分)
即: (4分)
(4分)
(2)解:
= (6分)
(6分)
当 为常数项时,即:
为常数项时,即: ,得
,得 5(8分)
5(8分)
 (9分)
(9分)
(3) 解:分类取第一式:
当第一式取1时
 (11分)
(11分)
当第一式取x时 (12分)
(12分)
当第一式取 时
时
 (13分)
(13分)
即: 的系数为210+120+45=375 (14分)
的系数为210+120+45=375 (14分)
第二问中,对于二项式定理的展开式的通项公式先写出,然后令未知数的次数为零即为所求的常数项。
第三问,利用配凑的思想得到,分为三种情况,当第一式取1时,当第一式去x时,当第一式取x2时,分别组合相乘得到。
(1)证明:左边=

=
 (2分)
(2分)=
 =
=
= 右边 (3分)
即:
 (4分)
(4分) (2)解:

=
 (6分)
(6分) 当
 为常数项时,即:
为常数项时,即: ,得
,得 5(8分)
5(8分) (9分)
(9分)(3) 解:分类取第一式:
当第一式取1时

 (11分)
(11分)当第一式取x时
 (12分)
(12分)当第一式取
 时
时
 (13分)
(13分)即:
 的系数为210+120+45=375 (14分)
的系数为210+120+45=375 (14分)
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
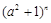 的展开式中各项系数之和等于
的展开式中各项系数之和等于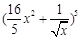 的展开式的常数项,并且
的展开式的常数项,并且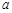 的值.
的值. 的展开式中
的展开式中 的系数为____________.
的系数为____________. 展开式中的常数项为
展开式中的常数项为 ,则实数
,则实数 =_______.
=_______. ,
, 的分解中最小的正整数是21,则
的分解中最小的正整数是21,则 ( )
( )



 展示式中不含
展示式中不含 项的系数的和为
项的系数的和为 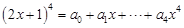 ,则
,则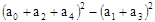 的值为__________.
的值为__________. 的展开式中,
的展开式中, 的系数与x的系数之和等于 ;
的系数与x的系数之和等于 ; 的展开式中,x的幂的指数是整数的项(有理项)共有 项
的展开式中,x的幂的指数是整数的项(有理项)共有 项