题目内容
4.执行如图所示的程序框图,若输出实数k的值为4,则框图中x的值是( )
| A. | 4 | B. | 16 | C. | 24 | D. | 120 |
分析 模拟执行程序框图,当S=24时,不满足条件S≤x,退出循环,输出K的值为4,对比各个选项可得框图中x的值是16.
解答 解:模拟执行程序框图,可得
K=1,S=1
满足条件S≤x,K=2,S=2
满足条件S≤x,K=3,S=6
满足条件S≤x,K=4,S=24
此时,不满足条件S≤x,退出循环,输出K的值为4,对比各个选项可得框图中x的值是16.
故选:B.
点评 本题主要考查了循环结构的程序框图,正确判断退出循环的条件是解题的关键,属于基础题.

练习册系列答案
相关题目
14.设min{p,q}表示p,q两者中的较小者,若函数f(x)=min{3-x,log2x},则满足f(x)≤$\frac{1}{2}$的x的集合为( )
| A. | (0,2]∪[$\frac{5}{2}$,+∞) | B. | [$\sqrt{2}$,$\frac{5}{2}$] | C. | (0,$\sqrt{2}$]∪[$\frac{5}{2}$,+∞) | D. | (0,$\sqrt{2}$)∪($\frac{5}{2}$,+∞) |
15.将函数y=sin($2x-\frac{π}{3})$的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
19.设直线x-3y+m=0(m≠0)与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线分别交于点A,B,若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$+1 |
9.已知函数f(x)=$\left\{\begin{array}{l}2lnx-x,x∈(0,2]\\ f(x-2),x∈(2,+∞)\end{array}$,a=log3162,b=$\frac{lg10000}{{{{log}_2}3}}$,则以下结论正确的是( )
| A. | f(a)<f(b)<0 | B. | f(b)<f(a)<0 | C. | 0<f(a)<f(b) | D. | 0<f(b)<f(a) |
16.在《爸爸去哪儿》第二季第四期中,假如村长给6位“萌娃”布置一项到A、B、C三个位置搜寻空投食物的任务,每两位“萌娃”搜寻一个位置.考虑到位置远近及年龄大小,Grace不去较远的A位置,多多不去较近的C位置,则不同的搜寻安排方案有( )
| A. | 20 种 | B. | 40 种 | C. | 42种 | D. | 48种 |
13.某正三棱柱的三视图如图所示,其中正(主)视图是正方形,该正三棱柱的侧视图的面积是( )
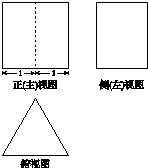

| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
13.a的值由如图程序框图算出,则二项式($\sqrt{x}$-$\frac{a}{x}$)9展开式的常数项为( )


| A. | T4=53×${C}_{9}^{3}$ | B. | T6=-55×${C}_{9}^{5}$ | C. | T5=74×${C}_{9}^{4}$ | D. | T4=-73×${C}_{9}^{3}$ |