题目内容
已知定义在区间 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图所示。
,其图象如图所示。
 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图所示。
,其图象如图所示。 
(Ⅰ)求函数 在
在 的表达式;
的表达式;
(Ⅱ)求方程 的解。
的解。
(Ⅲ)是否存在常数m的值,使得 在
在 上恒成立;若存在,求出m的取值范围;若不存在,请说明理由。
上恒成立;若存在,求出m的取值范围;若不存在,请说明理由。
 在
在 的表达式;
的表达式;(Ⅱ)求方程
 的解。
的解。(Ⅲ)是否存在常数m的值,使得
 在
在 上恒成立;若存在,求出m的取值范围;若不存在,请说明理由。
上恒成立;若存在,求出m的取值范围;若不存在,请说明理由。 解:(Ⅰ)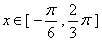 ,
,
∴A=1,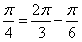 ,
,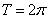 ,
,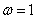 ,
,
且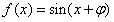 过
过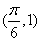 ,
,
∵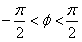 ,
,
∴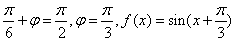 ,
,
当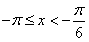 时,
时,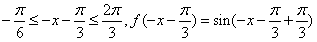 ,
,
而函数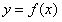 的图象关于
的图象关于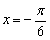 对称,则
对称,则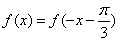 ,
,
即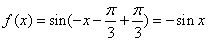 ,
,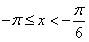 ,
,
∴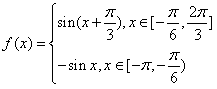 。
。
(Ⅱ)当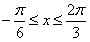 时,
时,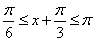 ,
,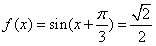 ,
,
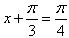 或
或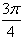 ,
,
∴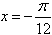 或
或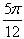 ;
;
当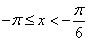 时,
时,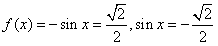 ,
,
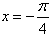 或
或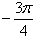 ,
,
∴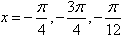 或
或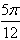 为所求。
为所求。
(Ⅲ)由条件得: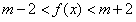 在
在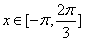 上恒成立,
上恒成立,
即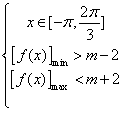 ,
,
由图象可得: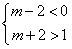 ,
,
∴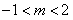 。
。
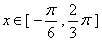 ,
,∴A=1,
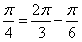 ,
,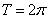 ,
,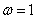 ,
,且
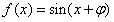 过
过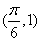 ,
,∵
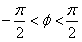 ,
,∴
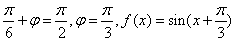 ,
,当
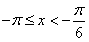 时,
时,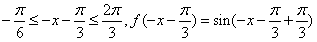 ,
,而函数
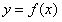 的图象关于
的图象关于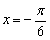 对称,则
对称,则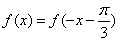 ,
,即
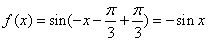 ,
,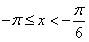 ,
,∴
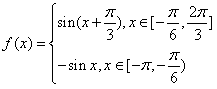 。
。(Ⅱ)当
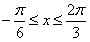 时,
时,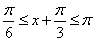 ,
,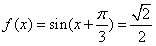 ,
,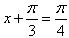 或
或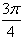 ,
,∴
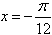 或
或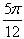 ;
;当
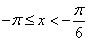 时,
时,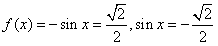 ,
,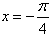 或
或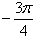 ,
,∴
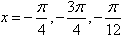 或
或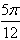 为所求。
为所求。(Ⅲ)由条件得:
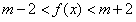 在
在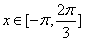 上恒成立,
上恒成立,即
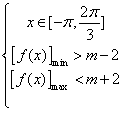 ,
,由图象可得:
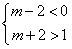 ,
,∴
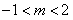 。
。
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)