题目内容
(本小题满分12分)
设函数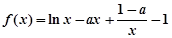 .
.
(Ⅰ)当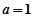 时,过原点的直线与函数
时,过原点的直线与函数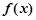 的图象相切于点P,求点P的坐标;
的图象相切于点P,求点P的坐标;
(Ⅱ)当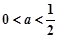 时,求函数
时,求函数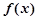 的单调区间;
的单调区间;
(Ⅲ)当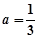 时,设函数
时,设函数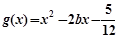 ,若对于
,若对于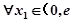 ],
],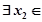 [0,1]
[0,1]
使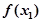 ≥
≥ 成立,求实数b的取值范围.(
成立,求实数b的取值范围.(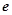 是自然对数的底,
是自然对数的底,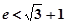 )。
)。
【答案】
函数 的定义域为
的定义域为 ,
, (2分)
(2分)
(Ⅰ)设点 ,当
,当 时,
时, ,则
,则 ,
, ,∴
,∴ (3分)
(3分)
解得 ,故点P 的坐标为
,故点P 的坐标为 (4分)
(4分)
(Ⅱ)

∵ ∴
∴ (5分)
(5分)
∴当 ,或
,或 时
时 ,当
,当 时,
时,
故当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;
;
单调递减区间为 ,
, (7分)
(7分)
(Ⅲ)当 时,
时, 由(Ⅱ)可知函数
由(Ⅱ)可知函数 在
在 上是减函数,在
上是减函数,在 上为增函数,在
上为增函数,在 上为减函数,且
上为减函数,且 ,
,
∵ ,又
,又 ,∴
,∴ ,
,
∴ ,故函数
,故函数 在
在 上的最小值为
上的最小值为 (9分)
(9分)
若对于 ,
, 使
使  ≥
≥ 成立
成立
 在
在 上的最小值不大于
上的最小值不大于
 在
在 上的最小值
上的最小值 (*)
(10分)
(*)
(10分)
又 ,
,
①当 时,
时, 在
在 上为增函数,
上为增函数, 与(*)矛盾
与(*)矛盾
②当 时,
时, ,由
,由 及
及 得,
得,

③当 时,
时, 在
在 上为减函数,
上为减函数, ,
,
此时
综上, 的取值范围是
的取值范围是
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目