题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() 为函数
为函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)讨论![]() 在定义域上的单调性.
在定义域上的单调性.
【答案】(Ⅰ) ![]() ;(Ⅱ) ①当
;(Ⅱ) ①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;②当
递减;②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;③当
递减;③当![]() 时,
时, ![]() 在
在![]() 内递减;④当
内递减;④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;
递增;
若![]() ,
, ![]() 递减.
递减.
【解析】试题分析:
(1)由题意可得![]() ,解得
,解得![]() .注意检验a的正确性.
.注意检验a的正确性.
(2)导函数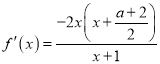 ,分类讨论可得:
,分类讨论可得:
①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
③当![]() 时,
时, ![]() 在
在![]() 内递减;
内递减;
④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减.
递减.
试题解析:
(Ⅰ)因为![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() .
.
经检验:当![]() 时,
时, ![]() 递增;
递增;
当![]() 时,
时, ![]() 递减.
递减.
所以![]() 在
在![]() 处取最大值.
处取最大值.
所以![]() 满足题意.
满足题意.
(Ⅱ) 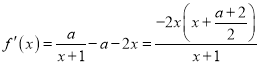 ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
又![]() 的定义域为
的定义域为![]() .
.
①当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
②当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
③当![]() ,即
,即![]() 时,
时,
![]() ,
, ![]() 在
在![]() 内递减;
内递减;
④当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减.
递减.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
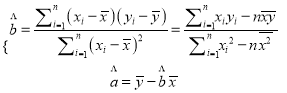
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.