题目内容
已知等比数列{an}的首项a1>0,公比q>0,前n项和为Sn.
(Ⅰ)试比较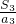 与
与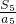 的大小;
的大小;
(Ⅱ)设{an}满足: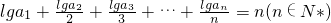 ,数列{bn}满足:
,数列{bn}满足: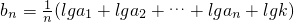 ,求数列{an}的通项公式和使数列{bn}成等差数列的正数k的值.
,求数列{an}的通项公式和使数列{bn}成等差数列的正数k的值.
解:(Ⅰ)①当q=1时, ,
,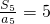 ,
,
∴ .
.
②当q>0且q≠1时,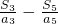 =
= ,
,
此时也有 .
.
综上可知: . …(4分)
. …(4分)
(Ⅱ)当n=1时,lga1=1?a1=10.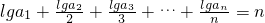 ,①
,①
∴当n≥2时,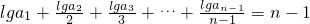 ,②
,②
将①-②得: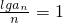 ,
,
∴lgan=n,∴an=10n.
综上可知:对n∈N*,an=10n. …(8分)
∴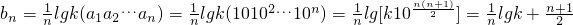 .
.
要使{bn}成等差数列,则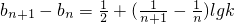 为常数,…(10分)
为常数,…(10分)
故只须lgk=0,即k=1. …(12分)
分析:(Ⅰ)对公比q的值进行分类讨论:①当q=1时, ,
,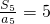 ,②当q>0且q≠1时,结合作差法比较大小即可得到:
,②当q>0且q≠1时,结合作差法比较大小即可得到: ;
;
(Ⅱ)先就n的值讨论:当n=1时;当n≥2时,两式相减,从而求出数列{an}的通项公式,再计算出数列{bn}的通项公式,要使{bn}成等差数列,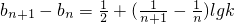 为常数从而求出k值.
为常数从而求出k值.
点评:本小题主要考查等差关系的确定、数列的求和、数列与不等式的综合等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
 ,
,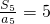 ,
,∴
 .
.②当q>0且q≠1时,
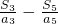 =
= ,
,此时也有
 .
.综上可知:
 . …(4分)
. …(4分)(Ⅱ)当n=1时,lga1=1?a1=10.
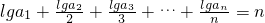 ,①
,①∴当n≥2时,
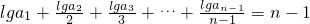 ,②
,②将①-②得:
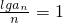 ,
,∴lgan=n,∴an=10n.
综上可知:对n∈N*,an=10n. …(8分)
∴
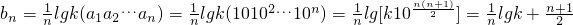 .
.要使{bn}成等差数列,则
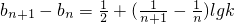 为常数,…(10分)
为常数,…(10分)故只须lgk=0,即k=1. …(12分)
分析:(Ⅰ)对公比q的值进行分类讨论:①当q=1时,
 ,
,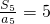 ,②当q>0且q≠1时,结合作差法比较大小即可得到:
,②当q>0且q≠1时,结合作差法比较大小即可得到: ;
;(Ⅱ)先就n的值讨论:当n=1时;当n≥2时,两式相减,从而求出数列{an}的通项公式,再计算出数列{bn}的通项公式,要使{bn}成等差数列,
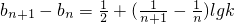 为常数从而求出k值.
为常数从而求出k值.点评:本小题主要考查等差关系的确定、数列的求和、数列与不等式的综合等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目