题目内容
设A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
A
解法一:由已知得f-1(x)=loga(x+![]() )>1=logaa,
)>1=logaa,
∴x+![]() >a,∴
>a,∴![]() >a-x.
>a-x.
又![]() >a-x
>a-x![]() a-x≤0或
a-x≤0或![]()
![]() x≥a或
x≥a或![]() <x<a
<x<a![]() x>
x>![]() ,故选A.
,故选A.
解法二:f(x)=![]() (ax-a-x)(a>1),
(ax-a-x)(a>1),
当a>1时,y=ax单增;当a>1时,y=a-x单减.
∴f(x)=![]() (ax-a-x)单增.∴f-1(x)也单增.
(ax-a-x)单增.∴f-1(x)也单增.
f-1(x)>1说明反函数的值域是(1,+∞),即原函数f(x)的定义域是(1,+∞).
求f-1(x)>1中x的取值范围,即求反函数的x的取值范围,只要求原函数f(x)在(1,+∞)上的值域.
又f(x)单增,∴f(x)>f(1),即f(x)>![]() .
.
∴f-1(x)>1中的x>![]() .故选A.
.故选A.

练习册系列答案
相关题目
已设 是函数
是函数 的反函数,若
的反函数,若 ,则f(a+b)的值为
,则f(a+b)的值为
| A.1 | B.2 | C.3 | D. |
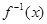 是函数
是函数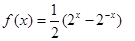 的反函数,则
的反函数,则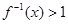 的解集为
的解集为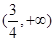 B.
B. C.
C.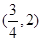 D.
D.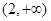
 是函数
是函数 的反函数,若
的反函数,若 ,则f(a+b)的值为
,则f(a+b)的值为

 是函数
是函数 的反函数,则使
的反函数,则使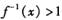 成立的x的取值范围是( )
成立的x的取值范围是( ) ,
, ) B.
(
) B.
( ,
, ) C.
(O,
) C.
(O, ) D.
(
) D.
( ,0)
,0)