题目内容
设曲线C:y=
(x≥0),直线y=0及x=t(t>0)所围成的封闭图形的面积为S(t),则S′(2)=
.
| x |
| 2 |
| 2 |
分析:由图形可知求出x从0到t,函数y=
(x≥0)上的定积分即为曲线C:y=
(x≥0),直线y=0及x=t(t>0)所围成的封闭图形的面积,再计算S′(2)的值.
| x |
| x |
解答: 解:由定积分在求面积中的应用可知,
解:由定积分在求面积中的应用可知,
曲线C:y=
(x≥0),直线y=0及x=t(t>0)所围成的封闭图形的面积设为S,
则S=∫0t
dx=
x
|0t=
t
,
S′(2)=
|
=
故答案为:
.
 解:由定积分在求面积中的应用可知,
解:由定积分在求面积中的应用可知,曲线C:y=
| x |
则S=∫0t
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
S′(2)=
| t |
t=2 |
| 2 |
故答案为:
| 2 |
点评:考查学生会利用定积分求平面图形面积,会利用数形结合的数学思想来解决实际问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
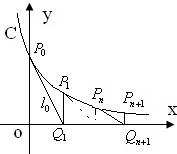 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).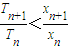 (n∈N+).
(n∈N+).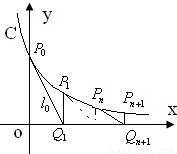
 (n∈N+).
(n∈N+).