题目内容
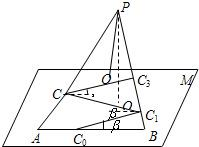 某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2Km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2Km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=| 2 |
| 5 |
| 1 |
| 4 |
(1)试问:垂直高度每升高100米,盘山公路需修建多长?若修建盘山公路至半山腰(高度为山高的一半),在半山腰的中心Q处修建上山缆车索道站,索道PQ依山而建(与山坡面平行,离坡面高度忽略不计),问盘山公路的长度和索道的长度各是多少?
(2)若修建盘山公路为xKm,其造价为
| x2+100 |
| 2 |
问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
分析:(1)在盘山公路上取一个点,作出该点到平面的垂线,再利用三垂线定理作出二面角棱的垂线,连接两个垂足,最后结合直角三角形内三角函数的定义可求出索道长与山高的倍数关系,得出结论;
(2)设盘山公路修至山高的距离为x,在(1)的条件下,结合勾股定理建立关于x的函数,最后利用导数的符号得出此函数是先减后增的函数,极小值即为函数的最小值,从而得出最少总价对应的x.
(2)设盘山公路修至山高的距离为x,在(1)的条件下,结合勾股定理建立关于x的函数,最后利用导数的符号得出此函数是先减后增的函数,极小值即为函数的最小值,从而得出最少总价对应的x.
解答: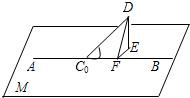 解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,
解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,
连接DF,易知DF⊥C0F.sin∠DFE=
,sin∠DC0F=
∵DF=
C0D,DE=
DF,∴DE=
C0D
所以盘山公路长度是山高的10倍,索道长是山高的
倍.所以垂直高度每升高100米,盘山公路需修建1000米.
从山脚至半山腰,盘山公路为10Km.从半山腰至山顶,索道长2.5Km.(6分)
(2)设盘山公路修至山高x(0<x<2)Km,则盘山公路长为10x,索道长
(2-x).
设总造价为y万元,则y=
a+
(2-x)•2
a
=(10
-5
x)a+10
a
令y′=
-5
=0,则x=1
当x∈(0,1)时y′<0,函数y单调递减
当x∈(1、2)时,y′>0,函数y单调递增
∴x=1,y有最小值,即修建盘山公路′至山高1Km时,总造价最小.(13分)
 解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,
解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,连接DF,易知DF⊥C0F.sin∠DFE=
| 2 |
| 5 |
| 1 |
| 4 |
∵DF=
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 10 |
所以盘山公路长度是山高的10倍,索道长是山高的
| 5 |
| 2 |
从山脚至半山腰,盘山公路为10Km.从半山腰至山顶,索道长2.5Km.(6分)
(2)设盘山公路修至山高x(0<x<2)Km,则盘山公路长为10x,索道长
| 5 |
| 2 |
设总造价为y万元,则y=
| (10x)2+100 |
| 5 |
| 2 |
| 2 |
=(10
| x2+1 |
| 2 |
| 2 |
令y′=
| 10x | ||
|
| 2 |
当x∈(0,1)时y′<0,函数y单调递减
当x∈(1、2)时,y′>0,函数y单调递增
∴x=1,y有最小值,即修建盘山公路′至山高1Km时,总造价最小.(13分)
点评:第一小问利用三垂线定理作辅助线,解决立体几何中与二面角有关的问题,是立几中常见的思路;第二小问处理带根号式子的函数,用导数研究单调性,不失为一个很好的工具.

练习册系列答案
相关题目
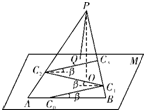 (2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
(2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
 .现从山脚的公路AB某处C开始修建与公路AB成β角的盘山公路CC1,C1C2,C2C3,…Cn-1Cn(如图所示).其中0<β<90°,sinβ=
.现从山脚的公路AB某处C开始修建与公路AB成β角的盘山公路CC1,C1C2,C2C3,…Cn-1Cn(如图所示).其中0<β<90°,sinβ=
 万元.而修建索道的造价为2
万元.而修建索道的造价为2 a元/Km.
a元/Km.
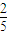 .现从山脚的水平公路AB某处C开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为
.现从山脚的水平公路AB某处C开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为 .试问:
.试问: a万元.修建索道的造价为2
a万元.修建索道的造价为2 a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.