题目内容
已知函数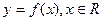 满足
满足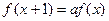 ,
,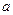 是不为
是不为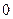 的实常数。
的实常数。
(1)若当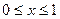 时,
时,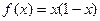 ,求函数
,求函数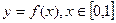 的值域;
的值域;
(2)在(1)的条件下,求函数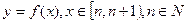 的解析式;
的解析式;
(3)若当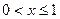 时,
时,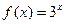 ,试研究函数
,试研究函数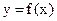 在区间
在区间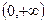 上是否可能是单调函数?
上是否可能是单调函数?
若可能,求出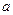 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。
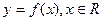 满足
满足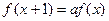 ,
,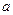 是不为
是不为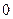 的实常数。
的实常数。(1)若当
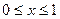 时,
时,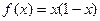 ,求函数
,求函数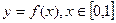 的值域;
的值域;(2)在(1)的条件下,求函数
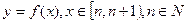 的解析式;
的解析式;(3)若当
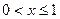 时,
时,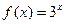 ,试研究函数
,试研究函数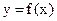 在区间
在区间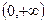 上是否可能是单调函数?
上是否可能是单调函数?若可能,求出
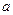 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
(1) 。
。
(2)当 ,
,
 ,
,
 。
。
(3)当 ,
, ,
,
 ;
;
显然 当
当 时是增函数,
时是增函数,
此时 ,
,
若函数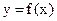 在区间
在区间 上是是单调增函数,则必有
上是是单调增函数,则必有 ,解得:
,解得: ;
;
显然当 时,函数
时,函数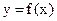 在区间
在区间 上不是单调函数;
上不是单调函数;
所以 。
。
 。
。(2)当
 ,
, ,
, 。
。(3)当
 ,
, ,
, ;
;显然
 当
当 时是增函数,
时是增函数,此时
 ,
,若函数
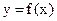 在区间
在区间 上是是单调增函数,则必有
上是是单调增函数,则必有 ,解得:
,解得: ;
;显然当
 时,函数
时,函数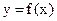 在区间
在区间 上不是单调函数;
上不是单调函数;所以
 。
。
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
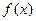 =
=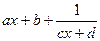 (
(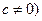 的对称中心为
的对称中心为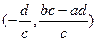
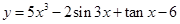 的图象的对称中心是
的图象的对称中心是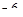 ,0)
,0)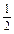 x,求使f(x)=-
x,求使f(x)=-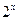 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=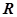 上的函数
上的函数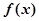 是奇函数且满足
是奇函数且满足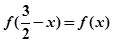 ,
,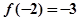 ,则
,则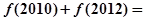 ( )
( )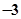
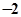
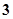
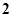
 ②
② ③
③
 ⑤
⑤ ⑥
⑥
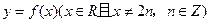 是周期为4的函数,
是周期为4的函数,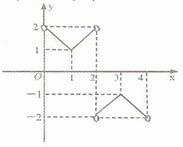
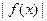 的值域是
的值域是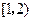 ;③关于
;③关于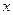 的方程
的方程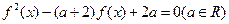 必有实根;
必有实根;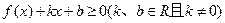 的解集非空。其中正确命题的个数为( ▲ )
的解集非空。其中正确命题的个数为( ▲ )