题目内容
已知 ,证明:
,证明: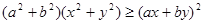 ,并利用上述结论求
,并利用上述结论求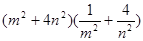 的最小值(其中
的最小值(其中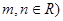 .
.
 ,证明:
,证明: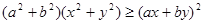 ,并利用上述结论求
,并利用上述结论求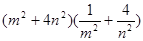 的最小值(其中
的最小值(其中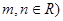 .
.见解析;
试题分析:可用作差比较;作差比较大小的关键是恰当变形,达到易于判断符号的目的,而常用的变形方法有配方法、因式分解等如本题中将
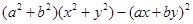 作差后关键就是变形确定符号,将其展开 后合并同类项得
作差后关键就是变形确定符号,将其展开 后合并同类项得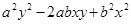 ,这个式子刚好就是一个完全平方
,这个式子刚好就是一个完全平方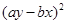 ,而
,而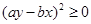 ,所以有
,所以有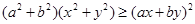 。也可以用分析法等来证明。分析法是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题。如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种证明方法叫做分析法。如本题中要证明
。也可以用分析法等来证明。分析法是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题。如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种证明方法叫做分析法。如本题中要证明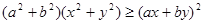 ,则找使得这个不等式成立的充分条件
,则找使得这个不等式成立的充分条件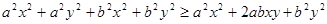 依次找下去,最后得到
依次找下去,最后得到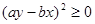 (显然成立),所以不等式得证。
(显然成立),所以不等式得证。试题解析:
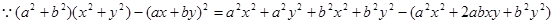
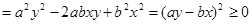 4分
4分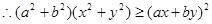 7分
7分(法二)要证明
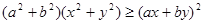
只要证
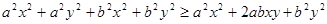 2分
2分即证
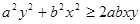 4分
4分即证
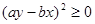 (显然成立)
(显然成立)故原不等式得证 7分
由不等式
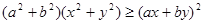 成立
成立知
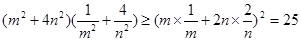 , 10分
, 10分即最小值为25,当且仅当
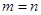 时等号成立。 13分
时等号成立。 13分
练习册系列答案
相关题目
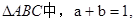
 ,且A.B.C成等差,求外接圆直径.
,且A.B.C成等差,求外接圆直径.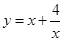
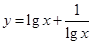
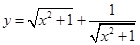

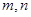 是正实数,且点
是正实数,且点 在曲线
在曲线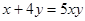 上,则
上,则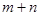 的最小值是 .
的最小值是 .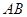 、
、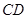 与桥面
与桥面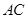 垂直,通过测量得知
垂直,通过测量得知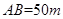 ,
,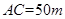 ,当
,当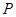 为
为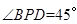 .
.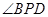 达到最大.
达到最大.
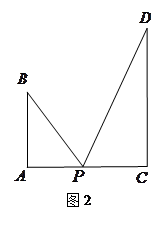
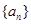 ,
,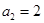 ,则其前三项和
,则其前三项和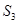 的取值范围是( )
的取值范围是( )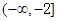
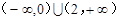
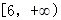
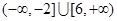
 +
+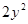 的最小值为______________.
的最小值为______________.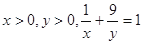 时,
时,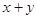 的最小值为( )
的最小值为( )