题目内容
已知平面向量a ,b=
,b= ,定义函数
,定义函数


(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)若函数 图象上的两点
图象上的两点 、
、 的横坐标分别为
的横坐标分别为 和
和 ,
, 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.
【答案】
(Ⅰ)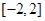 .
.
(Ⅱ)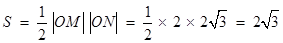 .
.
【解析】
试题分析:(Ⅰ)根据平面向量的坐标运算公式,利用三角公式化简得到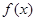
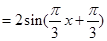 ,可得函数
,可得函数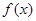 的值域为
的值域为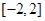 . (Ⅱ)通过确定
. (Ⅱ)通过确定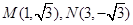 ,可考虑通过利用余弦定理确定三角形形状、利用向量的坐标运算,确定三角形形状等,计算三角形面积.
,可考虑通过利用余弦定理确定三角形形状、利用向量的坐标运算,确定三角形形状等,计算三角形面积.
试题解析:解:(Ⅰ)依题意得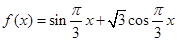 1分
1分
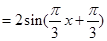 3分
3分
所以函数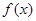 的值域为
的值域为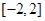 .
5分
.
5分
(Ⅱ)方法一 由(Ⅰ)知,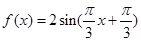
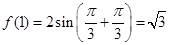 ,
,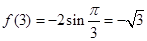 ,
6分
,
6分
从而 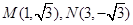 .
7分
.
7分
∴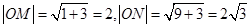 ,
,
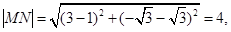 9分
9分
根据余弦定理得
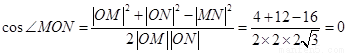 .
.
∴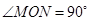 ,
10分
,
10分
△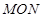 的面积为
的面积为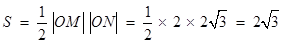 .
13分
.
13分
方法二 同方法一得: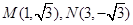 .
7分
.
7分
则 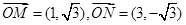 .
8分
.
8分
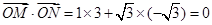 .
10分
.
10分
所以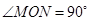 ,
, 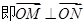
△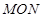 的面积为
的面积为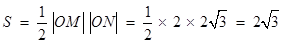 .
13分
.
13分
方法三 同方法一得: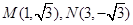 .
7分
.
7分
直线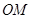 的方程为
的方程为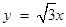 ,即
,即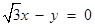 .
8分
.
8分
点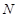 到直线
到直线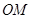 的距离为
的距离为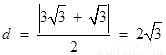 .
10分
.
10分
又因为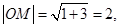 ,
11分
,
11分
所以△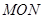 的面积为
的面积为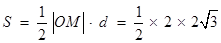
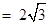 .
13分
.
13分
考点:1、平面向量的坐标运算,2、三角函数辅助角公式,3、三角形面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目