题目内容
在△ABC中,三内角A,B,C所对的边分别为a,b,c,若B=60°,c=(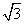 -1)a,
-1)a,
(Ⅰ)求角C的大小;
(Ⅱ)已知当x∈R时,函数f(x)=sinx(cosx+asinx)的最大值为1,求a的值。
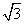 -1)a,
-1)a,(Ⅰ)求角C的大小;
(Ⅱ)已知当x∈R时,函数f(x)=sinx(cosx+asinx)的最大值为1,求a的值。
解:(Ⅰ)∵B=60°,
∴A+C=120°,A=120°-C,
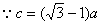 ,
,
∴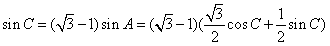 ,
,
整理得tanC=1,
∴C=45°;
(Ⅱ)f(x)=sinx(cosx+asinx)=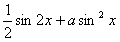
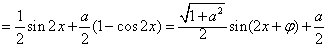 (其中tanφ=-a),
(其中tanφ=-a),
当x∈R时,函数f(x)的最大值为1,
∴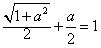 ,解得
,解得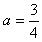 。
。
∴A+C=120°,A=120°-C,
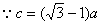 ,
,∴
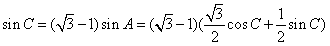 ,
,整理得tanC=1,
∴C=45°;
(Ⅱ)f(x)=sinx(cosx+asinx)=
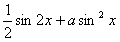
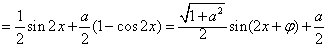 (其中tanφ=-a),
(其中tanφ=-a),当x∈R时,函数f(x)的最大值为1,
∴
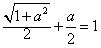 ,解得
,解得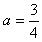 。
。
练习册系列答案
相关题目