题目内容
设a>0且a≠0,函数f(x)=| 1 | 2 |
(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;
(2)求函数f(x)的极值点.
分析:(1)由已知中函数 f(x)=
x2-(a+1)x+alnx,根据a=2,我们易求出f(3)及f′(3)的值,代入即可得到切线的斜率k=f′(3).
(2)由已知我们易求出函数的导函数,令导函数值为0,我们则求出导函数的零点,根据m>0,我们可将函数的定义域分成若干个区间,分别在每个区间上讨论导函数的符号,即可得到函数函数f(x)的极值点.
| 1 |
| 2 |
(2)由已知我们易求出函数的导函数,令导函数值为0,我们则求出导函数的零点,根据m>0,我们可将函数的定义域分成若干个区间,分别在每个区间上讨论导函数的符号,即可得到函数函数f(x)的极值点.
解答:解:(1)由已知x>0(2分)
当a=2时,f′(x)=x-3+
(4分)
所以f′(3)=
,
曲线y=f(x)在(3,f(3))处切线的斜率为
,(6分)
(2)f′(x)=x-(a+1)+
=
=
(8分)
由f'(x)=0得x=1或x=a,(9分)
①当0<a<1时,
当x∈(0,a)时,f'(x)>0,函数f(x)单调递增;
当x∈(a,1)时,f'(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,f'(x)>0,函数f(x)单调递增.
此时x=a是f(x)的极大值点,x=1是f(x)的极小值点(10分)
②当a>1时,
当x∈(0,1)时,f'(x)>0,函数f(x)单调递增;
当x∈(a,1)时,f'(x)<0,函数f(x)单调递减;
当x∈(a,+∞)时,f'(x)>0,函数f(x)单调递增
此时x=1是f(x)的极大值点,x=a是f(x)的极小值点(13分)
综上,当0<a<1时,x=a是f(x)的极大值点,x=1是f(x)的极小值点;
当a=1时,f(x)没有极值点;
当a>1时,x=1是f(x)的极大值点,x=a是f(x)的极小值点
当a=2时,f′(x)=x-3+
| 2 |
| x |
所以f′(3)=
| 2 |
| 3 |
曲线y=f(x)在(3,f(3))处切线的斜率为
| 2 |
| 3 |
(2)f′(x)=x-(a+1)+
| a |
| x |
| x2-(a+1)x+a |
| x |
| (x-1)(x-a) |
| x |
由f'(x)=0得x=1或x=a,(9分)
①当0<a<1时,
当x∈(0,a)时,f'(x)>0,函数f(x)单调递增;
当x∈(a,1)时,f'(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,f'(x)>0,函数f(x)单调递增.
此时x=a是f(x)的极大值点,x=1是f(x)的极小值点(10分)
②当a>1时,
当x∈(0,1)时,f'(x)>0,函数f(x)单调递增;
当x∈(a,1)时,f'(x)<0,函数f(x)单调递减;
当x∈(a,+∞)时,f'(x)>0,函数f(x)单调递增
此时x=1是f(x)的极大值点,x=a是f(x)的极小值点(13分)
综上,当0<a<1时,x=a是f(x)的极大值点,x=1是f(x)的极小值点;
当a=1时,f(x)没有极值点;
当a>1时,x=1是f(x)的极大值点,x=a是f(x)的极小值点
点评:本题考查的知识点是利用导数研究函数的单调性,利用导数研究曲线上某点切线方程,其中根据已知函数的解析式求出导函数的解析式是解答本题的关键,还考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函
,则称函 ; ②
; ② ; ③
; ③ .
. 等于( )
等于( ) B.
B. C.
C. D.无法确定
D.无法确定 ;
;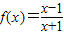 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.