Question

如图，四边形ABCD是矩形，SA⊥平面ABCD，SA=AB=1，AD=2，点M在线段BC上移动．
（1）若点M为BC的中点时，求直线SA与平面SDM所成角的正弦值；
（2）当BM等于何值时，二面角D-SM-B的大小为135°．

Answer 1

解：以AD，AB，AS为x，y，z轴，建立空间直角坐标系，
则A（0，0，0），B（0，1，0），S（0，0，1），D（2，0，0）．
（1）依题意有M（1，1，0），∴=（-1，1，0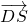），=（-2，0，1），
设平面SDM的法向量为=（x，y，z），则有，取x=1，得=（1，1，2）．
设直线SA与平面SDM所成角为θ，则sinθ=|cosθ|==，
故直线SA与平面SDM所成角的正弦值为．…6分
（2）设M（a，1，0）（0≤a≤2），则=（a-2，1，0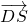），=（-2，0，1），
设平面SDM的法向量为=（x′，y′，z′），则有，
取x′=1，得=（1，2-a，2）．
设平面SMB的法向量为=（x″，y″，z″），
由=（a，0，0），=（0，-1，1），则有，取y″=1，得=（0，1，1）．
从而有|cos|=|cos135°|，即有=，
得（4-a）²=5+（2-a）²，解得，
即当BM=时，二面角D-SM-B的大小为135°．…13分．
分析：（1）以AD，AB，AS为x，y，z轴，建立空间直角坐标系，求出平面SDM的法向量，利用向量的夹角公式，可求直线SA与平面SDM所成角的正弦值；
（2）设出M的坐标，求出平面SDM的法向量、平面SMB的法向量，利用向量的夹角公式，即可求得结论．
点评：本题考查向量知识的运用，考查线面角，考查面面角，考查学生的计算能力，属于中档题．