题目内容
已知函数f(x)=tanx,x∈(0,
),若x1、x2∈(0,
),且x1≠x2,求证：
［f(x1)+f(x2)］＞f(
).
分析:题目中条件与结论之间的关系不明显，因此可以用分析法挖掘本题中的隐含条件，在证明过程中要注意分析法的格式与步骤.
证明：欲证［f(x1)+f(x2)］＞f(),
即证（tanx1+tanx2）＞tan,
只需证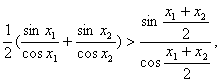
即证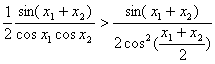
∵x1,x2∈(0,
),∴x1+x2∈(0,π).
∴sin(x1+x2)＞0,1+cos(x1+x2)＞0,
cosx1cosx2＞0.
∴只需证1+cos(x1+x2)＞2cosx1cosx2,
即证cos(x1-x2)＜1.
∵x1,x2∈(0,
),且x1≠x2,
∴cos(x1-x2)＜1显然成立.
∴原不等式成立.
绿色通道:
本题主要考查了三角函数与不等式证明的综合应用,在证明过程中注意角的取值范围及三角恒等变形公式的灵活运用.
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
(t∈R)在［1,2］上的最小值为
,P1(x1,y1),P2(x2,y2)是函数f(x)=
图象上不同两点,且线段P1P2的中点P的横坐标为
.
)(m∈N*,n=1,2,…,m),求数列{an}的前m项和Sm.