题目内容
过抛物线y=2x2的焦点的直线与抛物线交于A(x1,y1),B(x2,y2)则x1x2=
- A.-2
- B.

- C.-4
- D.
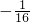
D
分析:抛物线y=2x2的标准方程是 ,它的焦点F(0,
,它的焦点F(0, ),设过焦点F(0,
),设过焦点F(0, )的直线是
)的直线是 ,由
,由 ,得
,得 ,由此能得到
,由此能得到 .
.
解答:∵抛物线y=2x2,
∴抛物线的标准方程是 ,它的焦点F(0,
,它的焦点F(0, ),
),
设过焦点F(0, )的直线是
)的直线是 ,
,
由 ,得
,得 ,
,
∵直线与抛物线交于A(x1,y1),B(x2,y2),
∴ .
.
故选D.
点评:本题考查直线和抛物线的位置关系,是基础题.解题时要认真审题,仔细解答,注意韦达定理的合理运用.
分析:抛物线y=2x2的标准方程是
 ,它的焦点F(0,
,它的焦点F(0, ),设过焦点F(0,
),设过焦点F(0, )的直线是
)的直线是 ,由
,由 ,得
,得 ,由此能得到
,由此能得到 .
.解答:∵抛物线y=2x2,
∴抛物线的标准方程是
 ,它的焦点F(0,
,它的焦点F(0, ),
),设过焦点F(0,
 )的直线是
)的直线是 ,
,由
 ,得
,得 ,
,∵直线与抛物线交于A(x1,y1),B(x2,y2),
∴
 .
.故选D.
点评:本题考查直线和抛物线的位置关系,是基础题.解题时要认真审题,仔细解答,注意韦达定理的合理运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目