题目内容
等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，
；则C的实轴长为________．
4
分析：设出双曲线方程，求出抛物线的准线方程，利用，即可求得结论．
解答：设等轴双曲线C的方程为x2-y2=λ．（1）
∵抛物线y2=16x，2p=16，p=8，∴
=4．
∴抛物线的准线方程为x=-4．
设等轴双曲线与抛物线的准线x=-4的两个交点A（-4，y），B（-4，-y）（y＞0），
则|AB|=|y-（-y）|=2y=4
，∴y=2．
将x=-4，y=2代入（1），得（-4）2-（2）2=λ，∴λ=4
∴等轴双曲线C的方程为x2-y2=4，即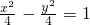
∴C的实轴长为4．
故答案为：4
点评：本题考查抛物线，双曲线的几何性质，考查学生的计算能力，属于基础题．
分析：设出双曲线方程，求出抛物线的准线方程，利用
，即可求得结论．解答：设等轴双曲线C的方程为x2-y2=λ．（1）
∵抛物线y2=16x，2p=16，p=8，∴
=4．∴抛物线的准线方程为x=-4．
设等轴双曲线与抛物线的准线x=-4的两个交点A（-4，y），B（-4，-y）（y＞0），
则|AB|=|y-（-y）|=2y=4
，∴y=2．将x=-4，y=2
代入（1），得（-4）2-（2）2=λ，∴λ=4∴等轴双曲线C的方程为x2-y2=4，即
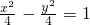
∴C的实轴长为4．
故答案为：4
点评：本题考查抛物线，双曲线的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目