题目内容
已知圆C与y轴交于两点M(0,-2),N(0,2),且圆心C在直线2x-y-6=0上.(1)求圆C的方程;
(2)过圆C的圆心C作一直线,使它夹在两直线l1:2x-y-2=0和l2:x+y+3=0间的线段AB恰好被点C所平分,求此直线的方程.
分析:(1)先由M,N的坐标确定圆心C的纵坐标为0,再根据圆心C在直线2x-y-6=0上,所以x=3,最后确定圆的半径,从而求出圆的方程;(2)先假设直线AB的方程为y=k(x-3),分别与l1,l2联立,利用中点坐标公式可求,同时注意斜率不存在情况的验证.
解答:解:(1)因为圆C与y轴交于两点M(0,-2),N(0,2),所以圆心C的纵坐标为0.
又因为圆心C在直线2x-y-6=0上,所以x=3.所以圆心C(3,0),半径|MC|=
=
.
所以圆C的方程为(x-3)2+y2=13.
(2)由(1)知圆心C(3,0),设A点的纵坐标为y1,B点的纵坐标为y2,
直线AB的斜率为k,则直线AB的方程为y=k(x-3),分别与l1,l2联立得
解得y1=
.
解得y2=
.由中点坐标公式,有
(y1+y2)=0.即
+
=0.所以k=8.
故所求直线方程为y=8(x-3).即8x-y-24=0.
当k不存在时,过点C(3,0)的直线方程为x=3与l1交点为(3,4),与l2交点为(3,-6),
其中点(3,-1)与圆心C(3,0)不符,故x=3不是所求直线.
又因为圆心C在直线2x-y-6=0上,所以x=3.所以圆心C(3,0),半径|MC|=
| 32+22 |
| 13 |
所以圆C的方程为(x-3)2+y2=13.
(2)由(1)知圆心C(3,0),设A点的纵坐标为y1,B点的纵坐标为y2,
直线AB的斜率为k,则直线AB的方程为y=k(x-3),分别与l1,l2联立得
|
| 4k |
| k-2 |
|
| -6k |
| k+1 |
| 1 |
| 2 |
| 4k |
| k-2 |
| -6k |
| k+1 |
故所求直线方程为y=8(x-3).即8x-y-24=0.
当k不存在时,过点C(3,0)的直线方程为x=3与l1交点为(3,4),与l2交点为(3,-6),
其中点(3,-1)与圆心C(3,0)不符,故x=3不是所求直线.
点评:本题考查圆的标准方程的求解,关键是确定圆心的坐标和半径,(2)利用设而不求法,应注意分类讨论思想的应用

练习册系列答案
相关题目
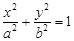 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且经过点P(1,
,且经过点P(1,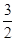 )。
)。