题目内容
正方形ABCD中，E为AB中点，F为BC中点，将△AED、△BEF及△DCF分别沿DE、EF、DF折起，使A、B、C点重合于P点．
（1）求证：PD⊥EF；
（2）求PD与平面DEF所成角的余弦值的大小．
（1）求证：PD⊥EF；
（2）求PD与平面DEF所成角的余弦值的大小．
证明：（1）∵DP⊥PF，DP⊥PE
∴DP⊥平面PEF
∴PD⊥EF
（2）取EF中点G，连DG，作PH⊥DG于H
∵E、F为中点
∴△ADE≌△CDF，故DE=DF，从而DG⊥EF
同理：EF⊥PG
又PG∩DG=G
∴EF⊥平面PDG，故EF⊥PH，从而PH⊥平面DEF
∴PD与平面DEF所成角为∠PDG
设正方形ABCD边长为2，则
PD=2，DE=DF=
，EF=
，DG=
在Rt△PDG中，cos∠PDG=
=
=
∴DP⊥平面PEF
∴PD⊥EF
（2）取EF中点G，连DG，作PH⊥DG于H
∵E、F为中点
∴△ADE≌△CDF，故DE=DF，从而DG⊥EF
同理：EF⊥PG
又PG∩DG=G
∴EF⊥平面PDG，故EF⊥PH，从而PH⊥平面DEF
∴PD与平面DEF所成角为∠PDG
设正方形ABCD边长为2，则
PD=2，DE=DF=
| 5 |
| 2 |
| 3 | ||
|
在Rt△PDG中，cos∠PDG=
| PD |
| DG |
| 2 | ||||
|
2
| ||
| 3 |
练习册系列答案
相关题目
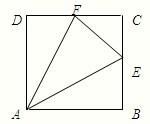如图，正方形ABCD中，E，F分别为BC，CD的中点，设∠EAF=θ，则cosθ=
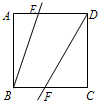（2012•浙江模拟）如图，在正方形ABCD中，E，F分别为线段AD，BC上的点，∠ABE=20°，∠CDF=30°．将△ABE绕直线BE、△CDF绕直线CD各自独立旋转一周，则在所有旋转过程中，直线AB与直线DF所成角的最大值为