题目内容
已知数列{an}为等差数列,公差d≠0,由{an}中的部分项组成的数列
a![]() ,a
,a![]() ,…,a
,…,a![]() ,…为等比数列,其中b1=1,b2=5,b3=17.
,…为等比数列,其中b1=1,b2=5,b3=17.
(1)求数列{bn}的通项公式;
(2)记Tn=C![]() b1+C
b1+C![]() b2+C
b2+C![]() b3+…+C
b3+…+C![]() bn,求
bn,求![]() .
.
(1) bn=2·3n-1-1 (2)![]()
解析:
(1)由题意知a52=a1·a17,即(a1+4d)2=a1(a1+16d)![]() a1d=2d2,
a1d=2d2,
∵d≠0,∴a1=2d,数列{![]() }的公比q=
}的公比q=![]() =3,
=3,
∴![]() =a1·3n-1 ①
=a1·3n-1 ①
又![]() =a1+(bn-1)d=
=a1+(bn-1)d=![]() ②
②
由①②得a1·3n-1=![]() ·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
(2)Tn=C![]() b1+C
b1+C![]() b2+…+C
b2+…+C![]() bn
bn
=C![]() (2·30-1)+C
(2·30-1)+C![]() ·(2·31-1)+…+C
·(2·31-1)+…+C![]() (2·3n-1-1)
(2·3n-1-1)
=![]() (C
(C![]() +C
+C![]() ·32+…+C
·32+…+C![]() ·3n)-(C
·3n)-(C![]() +C
+C![]() +…+C
+…+C![]() )
)
=![]() [(1+3)n-1]-(2n-1)=
[(1+3)n-1]-(2n-1)= ![]() ·4n-2n+
·4n-2n+![]() ,
,


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

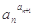 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4