题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，已知B=60°，C=75°，a=4，则b= ．
【答案】分析：先利用三角形的内角和及B，C的值求得A，进而利用正弦定理和a的值求得b．
解答：解：∵B=60°，C=75°
∴A=180°-60°-75°=45°，由正弦定理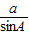
=
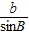得
=
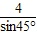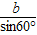，解得b=2
．
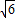故答案为：2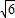
点评：本题主要考查了正弦定理的应用．正弦定理的基本公式及其变形公式是解三角形问题中常用的定理，平时应注意熟练记忆．
解答：解：∵B=60°，C=75°
∴A=180°-60°-75°=45°，由正弦定理
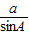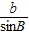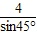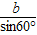=得=，解得b=2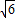．故答案为：2
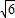
点评：本题主要考查了正弦定理的应用．正弦定理的基本公式及其变形公式是解三角形问题中常用的定理，平时应注意熟练记忆．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |