Question

将数列中的所有项按每一行比上一行多两项的规则排成如下数表：

已知表中的第一列数构成一个等差数列, 记为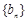, 且, 表中每一行正中间一个数构成数列, 其前n项和为.
(1)求数列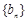的通项公式；(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且.①求；②记, 若集合M的元素个数为3, 求实数的取值范围.

Answer 1

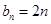（1）；（2）.

解析试题分析：(1)因为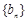为等差数列，且已知，用基本量法，设公差为d，有,解得，所以数列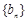的通项公式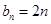；（2）①设每一行组成的等比数列的公比为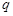,且前n行共有个数，有,可解得，因此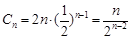，以下用错位相减法求；②由第①小题已知所以，令，可验证时，有，因为的元素个数3，所以.
试题解析：（1）；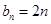
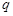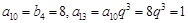（2）①设每一行组成的等比数列的公比为,由于前n行共有个数,且,所以,得
因此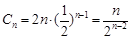


两式相减得
得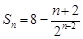
②由①知
设,计算得
且
当时,
的元素个数3
.
考点：基本量法求通项公式，错位相减法，方程与函数的思想，综合解决问题的能力.