题目内容
已知函数
在区间（0，1）上不是单调函数，则实数a的取值范围是（ ）A．（0，2）
B．[0，1）
C．（0，+∞）
D．（2，+∞）
【答案】分析：先对函数f（x）求导，根据函数
在区间（0，1）上不是单调函数，故f'（x）=ax2-x-1=0在区间（0，1）上有正有负，即函数f'（x）=0有解，从而得到答案．
解答：解：∵
∴f'（x）=ax2-x-1
∵函数
在区间（0，1）上不是单调函数
∴f'（x）=ax2-x-1=0在区间（0，1）上有根
∴当a=0时，x=-1不满足条件
当a＞0时，∵f'（0）=-1＜0，
∴f'（1）=a-2＞0，
∴a＞2
故选D．
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．
在区间（0，1）上不是单调函数，故f'（x）=ax2-x-1=0在区间（0，1）上有正有负，即函数f'（x）=0有解，从而得到答案．解答：解：∵
∴f'（x）=ax2-x-1
∵函数
在区间（0，1）上不是单调函数∴f'（x）=ax2-x-1=0在区间（0，1）上有根
∴当a=0时，x=-1不满足条件
当a＞0时，∵f'（0）=-1＜0，
∴f'（1）=a-2＞0，
∴a＞2
故选D．
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
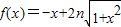在区间（0，∞）上的最小值是an（n∈N*）．
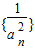的前n项的和，求
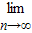Sn的值；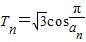
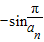，试比较Tn与Tn+1的大小．
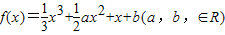在区间（0，1）内取得极大值，在区间（1，2）内取得极小值，则a的取值范围为（ ）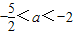
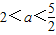
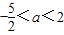
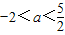
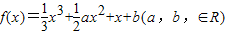在区间（0，1）内取得极大值，在区间（1，2）内取得极小值，则a的取值范围为（ ）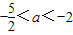
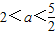
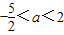
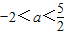
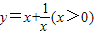在区间（0，1]上单调递减，在区间[1，+∞）上单调递增．若
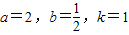，求函数f（x）的单调区间．