题目内容
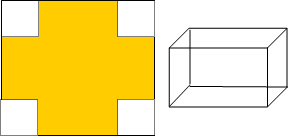
 如图所示,有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,求剪去的小正方形的边长及容积最大值.
如图所示,有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,求剪去的小正方形的边长及容积最大值.分析:列出容积与小正方形的边长的函数关系,建立实际问题的函数模型,利用导数作为工具求解该最值问题.
解答:解:设剪去的小正方形的边长为a,
则纸盒的容积为V=a(8-2a)(5-2a),(0<a<
)
∴V=4a3-26a2+40a,
∴V′=12a2-52a+40=4(a-1)(3a-10)
∴0<a<1,V′>0;
1<a<
,V′<0,
∴函数在(0,1)上单调递增,在(1,
)上单调递减,
∴a=1时,函数取得极大值,且为最大值,
∴剪去的小正方形的边长为1,容积最大值为18.
则纸盒的容积为V=a(8-2a)(5-2a),(0<a<
| 5 |
| 2 |
∴V=4a3-26a2+40a,
∴V′=12a2-52a+40=4(a-1)(3a-10)
∴0<a<1,V′>0;
1<a<
| 5 |
| 2 |
∴函数在(0,1)上单调递增,在(1,
| 5 |
| 2 |
∴a=1时,函数取得极大值,且为最大值,
∴剪去的小正方形的边长为1,容积最大值为18.
点评:本题考查函数的应用,考查函数模型的工具作用,考查求函数最值的导数思想,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目