如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值.则( )A.△A1B1C1和△A2B2C2都是锐角三角形B.△A1B1C1和△A2B2C2都是钝角三角形C.△A1B1C1是钝角三角形.△A2B2C2是锐角三角形D.△A1B1C1是锐角三角形.△A2B2C2是钝角三角形题目和参考答案——青夏教育精英家教网—

题目内容

如果△A₁B₁C₁的三个内角的余弦值分别等于△A₂B₂C₂的三个内角的正弦值，则(　　)

A.△A₁B₁C₁和△A₂B₂C₂都是锐角三角形

B.△A₁B₁C₁和△A₂B₂C₂都是钝角三角形

C.△A₁B₁C₁是钝角三角形，△A₂B₂C₂是锐角三角形

D.△A₁B₁C₁是锐角三角形，△A₂B₂C₂是钝角三角形

思路分析：本题主要考查诱导公式的应用，解题时可利用诱导公式将三角函数化为同名的三角函数.

解：△A₁B₁C₁的三个内角的余弦值均大于0，则△A₁B₁C₁是锐角三角形，若△A₂B₂C₂是锐角三角形，

由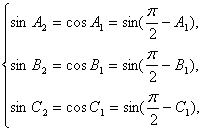得.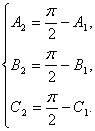

那么，A₂+B₂+C₂=，与三角形三个内角和为π相矛盾.

所以△A₂B₂C₂是钝角三角形.故选D.

答案:D

练习册系列答案

A、△A₁B₁C₁和△A₂B₂C₂都是锐角三角形

B、△A₁B₁C₁和△A₂B₂C₂都是钝角三角形

C、△A₁B₁C₁是钝角三角形，△A₂B₂C₂是锐角三角形

D、△A₁B₁C₁是锐角三角形，△A₂B₂C₂是钝角三角形

如果△A₁B₁C₁的三个内角的余弦值分别等于△A₂B₂C₂的三个内角的正弦值，则( )

A.△A₁B₁C₁和△A₂B₂C₂都是锐角三角形

B.△A₁B₁C₁和△A₂B₂C₂都是钝角三角形

C.△A₁B₁C₁是钝角三角形，△A₂B₂C₂是锐角三角形

D.△A₁B₁C₁是锐角三角形，△A₂B₂C₂是钝角三角形

如果△A₁B₁C₁的三个内角的余弦值分别等于△A₂B₂C₂的三个内角的正弦值,则( )

A.△A₁B₁C₁和△A₂B₂C₂都是锐角三角形

B.△A₁B₁C₁和△A₂B₂C₂都是钝角三角形

C.△A₁B₁C₁是钝角三角形,△A₂B₂C₂是锐角三角形

D.△A₁B₁C₁是锐角三角形,△A₂B₂C₂是钝角三角形

如果△A₁B₁C₁的三个内角的余弦值分别等于△A₂B₂C₂的三个内角的正弦值，则（）

A.△A₁B₁C₁和△A₂B₂C₂都是锐角三角形

B.△A₁B₁C₁和△A₂B₂C₂都是钝角三角形

C.△A₁B₁C₁是钝角三角形，△A₂B₂C₂是锐角三角形

D.△A₁B₁C₁是锐角三角形，△A₂B₂C₂是钝角三角形

给出下列命题：

①过一点与已知曲线相切的直线有且只有一条；②函数的对称中心是；③对任意实数a,b则④取一根长为3m的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不少于1m的概率是；⑤如果△A₁B₁C₁的三个内角的余弦值分别等于△A₂B₂C₂的三个内角的正弦值，则△A₁B₁C₁为锐角三角形，△A₂B₂C₂为钝角三角形.其中真命题的序号是（将所有真命题的序号都填上）.

试题分类