题目内容
已知
=3,求
.
分析:由已知条件先求a,b的值，再求所求的极限值.
解:由=1，可设ax2+bx+1=（x-1）（ax+c）.
∴ax2+bx+1=ax2+（c-a）x-c且（ax+c）=3
∴
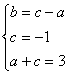
解得：c=-1,a=4,b=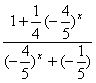-5
∴
=
=
=-5.
练习册系列答案
相关题目
=3,题目内容
已知=3,求.
分析:由已知条件先求a,b的值，再求所求的极限值.
解:由=1，可设ax2+bx+1=（x-1）（ax+c）.
∴ax2+bx+1=ax2+（c-a）x-c且（ax+c）=3
∴
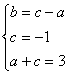
解得：c=-1,a=4,b=-5
∴=
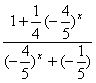==-5.
3,求
的值; 
+
=3,求a2+a-2的值.
+
=3,求
的值;
.
=3,求
的值.